Ovo poglavlje bavi se nalaženjem neodređenih
integrala (kraće: integrala), odnosno
anti-derivacija. Prije formalne definicije
neodređenog integrala, neformalno ćemo opisati osnovnu ideju.
Anti-derivacija zadane funkcije je funkcija čija je
derivacija jednaka zadanoj funkciji.
Na primjer, kako je
![]() , to je anti-derivacija funkcije
, to je anti-derivacija funkcije
![]() jednaka
jednaka ![]() .
Međutim, kako je derivacija konstante jednaka nuli,
to je i funkcija
.
Međutim, kako je derivacija konstante jednaka nuli,
to je i funkcija
![]() također anti-derivacija funkcije
također anti-derivacija funkcije
![]() za svaku konstantu
za svaku konstantu ![]() . Integral zadane funkcije je skup svih
njenih anti-derivacija, što zapisujemo kao
. Integral zadane funkcije je skup svih
njenih anti-derivacija, što zapisujemo kao
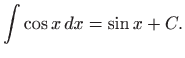
Zaključujemo da neke integrale možemo dobiti čitajući tablicu elementarnih derivacija (vidi1.1
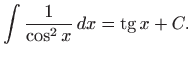
Međutim, integriranje je složeniji postupak od deriviranja. Također,
integral elementarne funkcije nije uvijek elementarna funkcija.
Naime, dok je svaku elementarnu funkciju lako derivirati jednostavnom
primjenom pravila deriviranja, pri čemu je derivacija opet elementarna
funkcija, kod integriranja to nije slučaj.
Tako je, na primjer,
![]() ,
dok recimo
,
dok recimo
![]() nije elementarna funkcija, odnosno ne
može se prikazati primjenjujući konačan broj puta zbrajanje, oduzimanje,
množenje, dijeljenje i komponiranje osnovnih elementarnih funkcija
(vidi
nije elementarna funkcija, odnosno ne
može se prikazati primjenjujući konačan broj puta zbrajanje, oduzimanje,
množenje, dijeljenje i komponiranje osnovnih elementarnih funkcija
(vidi
![]() M1, poglavlje 4.6.7). Integral ove funkcije može se
prikazati pomoću reda funkcija (poglavlje 1.8).
M1, poglavlje 4.6.7). Integral ove funkcije može se
prikazati pomoću reda funkcija (poglavlje 1.8).
U ovom poglavlju dat ćemo definiciju i osnovna svojstva integrala, opisati osnovne metode integriranja te postupke integriranja za nekoliko tipova funkcija (racionalne funkcije, racionalne funkcije trigonometrijskih funkcija i neke iracionalne funkcije). Opisat ćemo i postupak integriranja reda funkcija.