Funkciju
ima smisla promatrati samo u sljedećim slučajevima (uvedimo oznaku
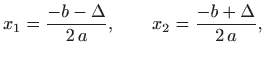
Integral oblika
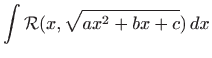
svodi se na jedan od tri jednostavnija integrala pomoću supstitucije1.5
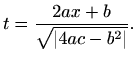
Za rješavanje tih integrala koristimo ili trigonometrijske ili Eulerove supstitucije:
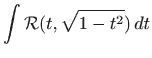 |
||||
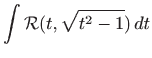 |
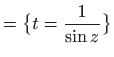 |
|||
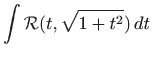 |
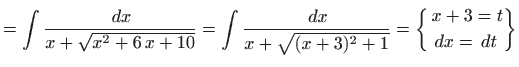 |
||
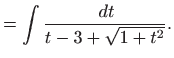 |
Eulerova supstitucija daje
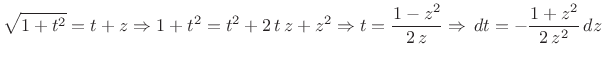
pa je
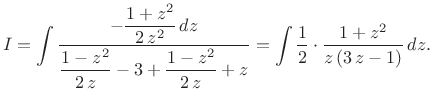
Dobiveni integral racionalne funkcije sada se riješi prema pravilima iz poglavlja 1.4.
Trigonometrijska supstitucija daje
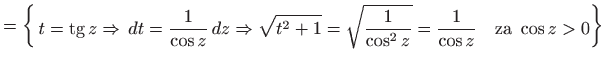 |
||
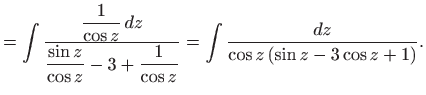 |
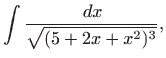 |
||
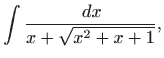 |
||
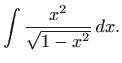 |