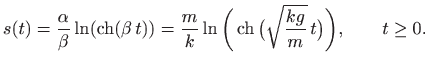Korištenjem integralnog računa iz ove glave i diferencijalnog računa
(vidi
![]() M1, poglavlje 5), možemo rješavati razne probleme u fizici
i tehnici, ili općenito prirodi, što je i svrha integralnog i
diferencijalnog računa. U ovom poglavlju iskoristit ćemo do sada
naučeno za rješavanje problema slobodnog pada.
M1, poglavlje 5), možemo rješavati razne probleme u fizici
i tehnici, ili općenito prirodi, što je i svrha integralnog i
diferencijalnog računa. U ovom poglavlju iskoristit ćemo do sada
naučeno za rješavanje problema slobodnog pada.
Ako pretpostavimo da je prilikom slobodnog pada otpor zraka proporcionalan kvadratu brzine, onda prema drugom Newtonovom zakonu vrijedi
pri čemu je
Izvest ćemo formulu za brzinu ![]() u ovisnosti o prijeđenom putu
u ovisnosti o prijeđenom putu ![]() ,
,
![]() (vidi sliku 1.2 za
(vidi sliku 1.2 za ![]() ).
).
Iz Newtonove formule slijedi
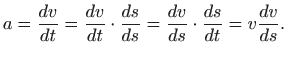
Kombinirajući dvije prethodne formule uz oznaku
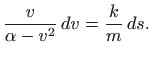
Integriranje obiju strana daje
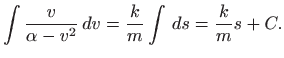
Integral na lijevoj strani riješimo supstitucijom
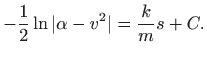
Iz formule (1.9) i činjenice da je ubrzanje pozitivno slijedi
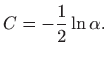
Dakle,
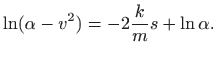
Svojstvo logaritma (vidi
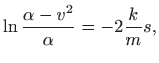
pa eksponenciranje daje
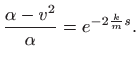
Rješavanje ove jednadžbe po
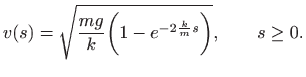
Vidimo kako se brzina ne može beskonačno povećavati jer je
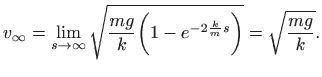
Isto smo mogli zaključiti i direktno iz formule (1.9) jer za tu vrijednost brzine ubrzanje iščezava.
Pogledajmo što se dogodi kada nema otpora zraka, odnosno za
![]() . Uvrštavanje daje neodređeni oblik,
. Uvrštavanje daje neodređeni oblik,
![]() .
Svojstvo neprekidnih funkcija (vidi
.
Svojstvo neprekidnih funkcija (vidi
![]() M1, teorem 4.7)
- u ovom slučaju drugi korijen - i L'Hospitalovo pravilo
(vidi
M1, teorem 4.7)
- u ovom slučaju drugi korijen - i L'Hospitalovo pravilo
(vidi
![]() M1, poglavlje 5.5.3) daju poznatu formulu
M1, poglavlje 5.5.3) daju poznatu formulu
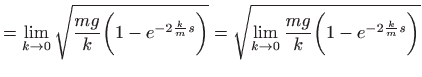 |
||
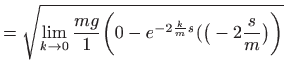 |
||
Integralni račun se također koristiti i kod izvođenja formule za put u ovisnosti o vremenu. Drugačijim pristupom, čiji izvod preskačemo, dobije se formula za brzinu kao funkciju vremena
gdje je
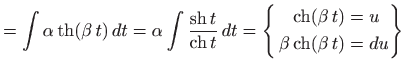 |
||
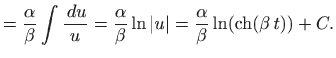 |
Dakle,