×   HOME
SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS
SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA
SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA
JAVA NETPLOT OCTAVE Traži ...
☰   matematika2
Eulerova metoda konačnih razlika     MATEMATIKA 2 - PREDAVANJA     Populacijska i logistička jednadžba


DIFERENCIJALNE JEDNADŽBE

Definicija 5.1   Diferencijalna jednadžba je jednadžba oblika

$\displaystyle F(x,y,y',y'',\ldots, y^{(n)})=0.$ (DJ)

Rješenje diferencijalne jednadžbe je svaka funkcija $ y=f(x)$ koja zadovoljava jednadžbu DJ na nekom skupu $ \mathcal{D}\subseteq{\mathbb{R}}$ . Red diferencijalne jednadžbe je red najviše derivacije koja se javlja u jednadžbi.

Najjednostavnije diferencijalne jednadžbe već smo rješavali: rješenje jednadžbe

$\displaystyle y'=f(x) $

je primitivna funkcija funkcije $ f(x)$ pa vrijedi

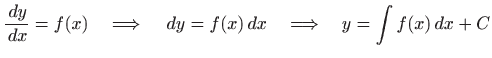
$\displaystyle \frac{ dy}{ dx}=f(x) \quad \Longrightarrow \quad dy=f(x) dx\quad \Longrightarrow \quad y=\int f(x) dx+C $

Ako želimo odrediti konstantu integracije $ C$ , treba biti zadan još jedan uvjet (vrijednost funkcije $ y(x_0)$ ili vrijednost derivacije $ y'(x_0)$ u nekoj točki $ x_0\in\mathcal{D}$ ).

Općenito, postupak rješavanja diferencijalne jednadžbe u sebi sadrži višekratno integriranje. Pri tome se u rješenju jednadžbe $ n$ -tog reda javlja $ n$ konstanti za čije je određivanje potrebno znati $ n$ uvjeta koje u odabranim točkama trebaju zadovoljavati funkcija $ y$ i/ili njene derivacije. Obično su uvjeti zadani u rubnim točkama područja u kojem promatramo diferencijalnu jednadžbu.

Diferencijalne jednadžbe su jedan od najvažnijih dijelova matematike uopće. Kako je derivacija mjera promjene, diferencijalnim jednadžbama se izražavaju i modeliraju mnogi prirodni zakoni.

Primjer 5.1   Promotrimo problem titranja mase obješene na oprugu (slika 5.1), pri čemu je $ x(t)$ položaj mase u trenutku $ t$ .

Slika: Titranje mase obješene na oprugu
\begin{figure}\centering \epsfig{file=slike/opr.eps,width=7cm} \end{figure}

Prema Hookeovom zakonu sila potrebna za održavanje opruge rastegnutom $ x$ jedinica udaljenosti od njene prirodne dužine proporcionalna je s $ x$ , $ F(x)=kx$ . Stoga je sila s kojom se opruga vraća u položaj ravnoteže jednaka $ -kx$ . S druge strane, prema Newtonovom drugom zakonu gibanja, sila je jednaka umnošku mase i ubrzanja. Izjednačavanje sila daje diferencijalnu jednadžbu

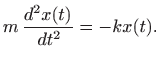
$\displaystyle m \frac{d^2x(t)}{ dt^2} = -kx(t). $

Odavde slijedi

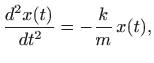
$\displaystyle \frac{d^2x(t)}{ dt^2} = -\frac{k}{m} x(t), $

odnosno, druga derivacije od $ x$ je proporcionalna $ x$ , ali ima obrnuti predznak. Znamo da funkcije sinus i kosinus imaju upravo to svojstvo. Kasnije ćemo pokazati da se sva rješenja ove jednadžbe mogu napisati kao određene kombinacije sinusa i kosinusa. Kako se radi o diferencijalnoj jednadžbi drugog reda, za određivanje konstanti potrebna su dva uvjeta. U ovom slučaju prirodni uvjeti su položaj i brzina u trenutku $ t=0$ , odnosno potrebno je zadati vrijednosti $ x(0)$ i $ x'(0)$ .

Primjer 5.2   Promotrimo strujni krug koji se sastoji od elektromotorne sile koja u trenutku $ t$ proizvodi napon od $ E(t)$ volta (V) i struju od $ I(t)$ ampera (A). U krugu se također nalazi otpor od $ R$ oma (Ohm) i zavojnica s induktivitetom $ L$ henrija (H) (slika 5.2).

Slika 5.2: Strujni krug
\begin{figure}\centering \epsfig{file=slike/stk.eps,width=4.4cm} \end{figure}

Prema Ohmovom zakonu pad napona na otporu jednak je $ RI$ . Pad napona na zavojnici jednak je $ L(dI/dt)$ . Prema Kirchoffovom zakonu zbroj padova napona jednak je naponu kojeg daje naponski izvor. Dakle,

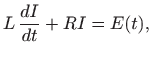
$\displaystyle L \frac{dI}{dt}+RI=E(t), $

što je diferencijalna jednadžba prvog reda koja modelira struju $ I$ u trenutku $ t$ . Riješimo zadanu jednadžbu uz (prirodan) uvjet da je struja u trenutku uključivanja naponskog izvora $ t=0$ jednaka nuli, $ I(0)=0$ . Uz oznake $ \alpha=R/L$ i $ \beta=1/L$ vrijedi

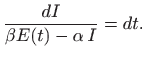
$\displaystyle \frac{dI}{\beta E(t)-\alpha I }=dt. $

Ako je elektromotorna sila konstantna, $ E(t)=E=konst.$ , onda integriranje obaju strana daje

$\displaystyle -\alpha \ln \vert\beta E -\alpha I\vert= t+C, $

odnosno

$\displaystyle \vert \beta E -\alpha I\vert=e^{-\alpha (t+C)}=e^{-\alpha C}e^{-\alpha t}, $

pa možemo pisati

$\displaystyle \beta E-\alpha I=A e^{-\alpha t}, $

pri čemu smo predznak izraza $ \beta E-\alpha I$ uključili u konstantu $ A$ . Dakle,

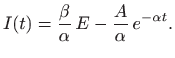
$\displaystyle I(t)= \frac{\beta}{\alpha} E -\frac{A}{\alpha} e^{-\alpha t}. $

Odredimo konstantu $ A$ : iz početnog uvjeta slijedi

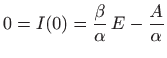
$\displaystyle 0=I(0)=\frac{\beta}{\alpha} E -\frac{A}{\alpha} $

pa je $ A=\beta E$ . Konačno,

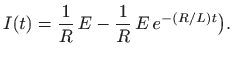
$\displaystyle I(t)=\frac{1}{R} E - \frac{1}{R} E e^{-(R/L) t}\big). $

Ako je, na primjer, $ L=4 \mathrm{H}$ , $ R=12 \mathrm{Ohm}$ i $ E(t)=60 \mathrm{V}$ , onda je

$\displaystyle I(t)=5-5 e^{-3 t}. $

Funkcija je prikazana na slici 5.3. Stacionarno stanje strujnog kruga je horizontalna asimptota

$\displaystyle \lim_{t\to\infty} I(t)=5 \mathrm{A}. $

Slika 5.3: Struja u strujnom krugu
\begin{figure}\centering \epsfig{file=slike/struja.eps,width=7.2cm} \end{figure}


Poglavlja

Eulerova metoda konačnih razlika     MATEMATIKA 2 - PREDAVANJA     Populacijska i logistička jednadžba