Neka ![]() označava broj jedinki neke populacije u trenutku
označava broj jedinki neke populacije u trenutku
![]() . Najjednostavniji model rasta populacije je sljedeći: stopa rasta
populacije proporcionalna je veličini populacije, odnosno promjena u populaciji
bit će veća što je u populaciji više jedinki.
Ovo je razumna pretpostavka za
populacije bakterija ili životinja u idealnim uvjetima (neograničeni resursi,
odgovarajuća prehrana, nepostojanje bolesti, nepostojanje prirodnih
neprijatelja).
. Najjednostavniji model rasta populacije je sljedeći: stopa rasta
populacije proporcionalna je veličini populacije, odnosno promjena u populaciji
bit će veća što je u populaciji više jedinki.
Ovo je razumna pretpostavka za
populacije bakterija ili životinja u idealnim uvjetima (neograničeni resursi,
odgovarajuća prehrana, nepostojanje bolesti, nepostojanje prirodnih
neprijatelja).
Kako je promjena populacije dana s
![]() , matematička formulacija rasta
populacije glasi
, matematička formulacija rasta
populacije glasi
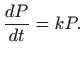
Ova diferencijalna jednadžba rješava se slično kao i jednadžba iz primjera 5.2:
Ako umjesto inicijalne populacije u trenutku
Konačno, uočimo sljedeće: ako je
|
|
Uzmemo li za početnu godinu ![]() , imamo
, imamo
Odredimo parametar
Dakle,
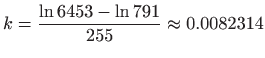
pa je
Funkcija
Funkcija ![]() prolazi, doduše, točkama
prolazi, doduše, točkama
![]() i
i
![]() , ali ne
opisuje dobro stvarni rast stanovništva. Razlog tome je jasan - jednostavni
model kojeg smo izabrali očito ne uključuje sve parametre koji utječu na rast
populacije. Međutim, ako se ograničimo samo na razdoblje od godine 1950. do
danas, onda je
, ali ne
opisuje dobro stvarni rast stanovništva. Razlog tome je jasan - jednostavni
model kojeg smo izabrali očito ne uključuje sve parametre koji utječu na rast
populacije. Međutim, ako se ograničimo samo na razdoblje od godine 1950. do
danas, onda je
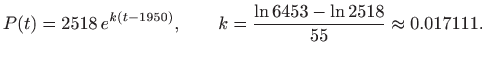
Na slici 5.5 vidimo da je sada preklapanje funkcije i stvarnih podataka puno bolje. Stopa rasta stanovništva je u tom razdoblju približno jednaka
Prvo je, kao i u prethodnom primjeru, potrebno utvrditi koeficijent ![]() , koji
će u ovom slučaju biti negativan jer se radi o "opadanju populacije". Vrijeme
poluraspada je vrijeme potrebno da se količina radioaktivne tvari svede na
polovicu. Dakle, imamo redom
, koji
će u ovom slučaju biti negativan jer se radi o "opadanju populacije". Vrijeme
poluraspada je vrijeme potrebno da se količina radioaktivne tvari svede na
polovicu. Dakle, imamo redom
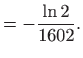 |
pa će laboratorij nakon sto godina imati
slijedi
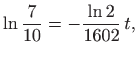
odnosno
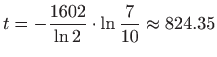
pa će laboratorij imati
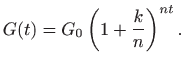
Naime, u
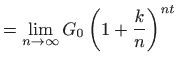 |
||
![$\displaystyle =G_0 \lim_{n\to\infty}\left[\left(1+\frac{k}{n}\right)^{n/k}\right]^{kt}$](img2731.gif) |
||
![$\displaystyle =G_0 \left[ \lim_{m\to\infty}\left(1+\frac{1}{m}\right)^{m}\right]^{kt}$](img2732.gif) |
Na primjer, uz početni iznos od 1000 kuna i godišnju kamatu od 6% nakon tri godine glavnica uz jednogodišnje, polugodišnje, kvartalno, mjesečno, dnevno i neprekidno ukamaćivanje iznosi redom
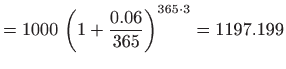 |
||
Prirodni sustavi zbog svojih ograničenja ne mogu prihvatiti
neograničenu populaciju pa često razmatramo sljedeći slučaj:
populacija ![]() u početku raste eksponencijalno sa stopom rasta
u početku raste eksponencijalno sa stopom rasta ![]() , ali se taj
rast smanjuje kako se populacija približava maksimalnom (nosivom) kapacitetu
sustava
, ali se taj
rast smanjuje kako se populacija približava maksimalnom (nosivom) kapacitetu
sustava ![]() . Matematički takvo ponašanje možemo modelirati logističkom
jednadžbom:
. Matematički takvo ponašanje možemo modelirati logističkom
jednadžbom:
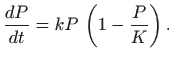
Mehanizam jednadžbe je sljedeći: kada ja populacija
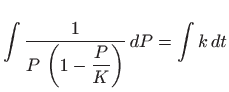 |
||
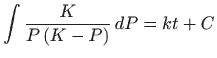 |
||
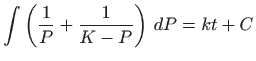 |
||
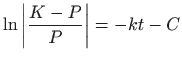 |
||
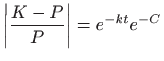 |
||
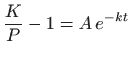 |
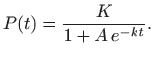
Konstantu
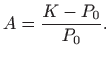
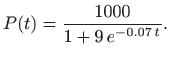
Tako ćemo, na primjer, nakon 12 sati imati
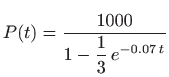
pa ćemo nakon 12 sati imati