Postupak opisan u prethodnim poglavljima se, uz odgovarajuće izmjene,
može primijeniti i za ispitivanje toka parametarski zadane
funkcije.
Međutim, kako su kod parametarski zadanih funkcija varijable ![]() i
i ![]() ravnopravne, postupak ispitivanja takvih funkcija može biti složeniji od
ispitivanja eksplicitno zadanih funkcija.
ravnopravne, postupak ispitivanja takvih funkcija može biti složeniji od
ispitivanja eksplicitno zadanih funkcija.
Ispitivanje toka parametarski zadane funkcije ilustrirat ćemo na primjeru Descartesovog lista iz primjera 4.2, 4.4 i 4.12, koji je u parametarskom obliku zadan s
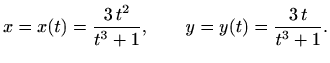
Ispitajmo parnost zadane funkcije po prethodnoj definiciji.
Pretpostavimo da je funkcija parna. Ako je točka
![]() element
grafa funkcije, tada je i točka
element
grafa funkcije, tada je i točka
![]() također element grafa
funkcije. No, tada postoji
također element grafa
funkcije. No, tada postoji
![]() takav da je
takav da je
![]() . Uvrštavanje u definiciju funkcije daje
. Uvrštavanje u definiciju funkcije daje
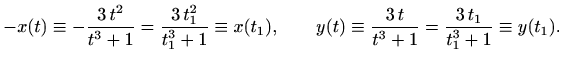
Gornje jednakosti su ispunjene samo za
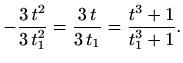
Nakon kraćenja prva jednakost povlači
Pretpostavimo sada da je funkcija neparna. Ako je točka
![]() element grafa funkcije, tada je i točka
element grafa funkcije, tada je i točka
![]() također element grafa funkcije.
No, tada postoji
također element grafa funkcije.
No, tada postoji
![]() takav da je
takav da je
![]() . Uvrštavanje u definiciju funkcije daje
. Uvrštavanje u definiciju funkcije daje
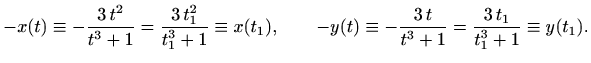
Kao i u prethodnom slučaju, gornje jednakosti su ispunjene samo za
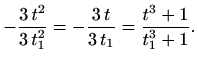
Nakon kraćenja prva jednakost povlači
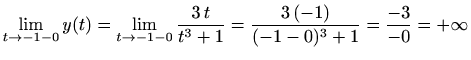
pa funkcija nema horizontalnu asimptotu u lijevoj strani. Slično,
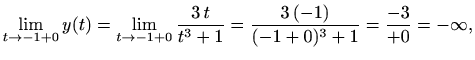
zaključujemo da funkcija nema horizontalnu asimptotu ni u desnoj strani.
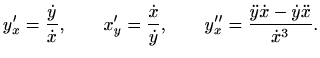
Zbog složenosti postupka, kod ispitivanje ekstrema i monotonosti potrebno je voditi računa o mnogim detaljima.
Nađimo ekstreme po ![]() . Vrijedi
. Vrijedi
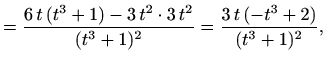 |
||
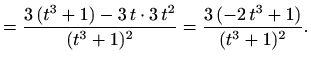 |
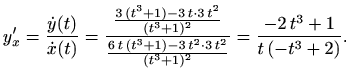
Po Teoremu o nužnim uvjetima ekstrema 5.12 imamo tri točke u kojima se mogu nalaziti lokalni ekstremi i to za vrijednosti parametra
Međutim, s ovim još nismo riješili status točaka ![]() i
i ![]() .
Pogledajmo sada ekstreme po
.
Pogledajmo sada ekstreme po ![]() . Vrijedi
. Vrijedi
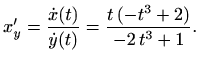
Očito je u okolinama točaka
Radi lakšeg praćenja prethodnog izlaganja, funkcije ![]() i
i ![]() te
njihove derivacije po parametru
te
njihove derivacije po parametru ![]() i po
i po ![]() i
i ![]() prikazane su na
slikama 5.15, 5.16 i 5.17.
Vidimo da je prilikom ispitivanja toka parametarski zadane funkcije
korisno detaljno ispitati i tokove funkcija
prikazane su na
slikama 5.15, 5.16 i 5.17.
Vidimo da je prilikom ispitivanja toka parametarski zadane funkcije
korisno detaljno ispitati i tokove funkcija ![]() i
i ![]() .
To je u ovom slučaju jednostavno, jer se radi o racionalnim
funkcijama.
.
To je u ovom slučaju jednostavno, jer se radi o racionalnim
funkcijama.
Ove slike nam daju još neke korisne informacije. Tako iz oblika
funkcija ![]() i
i ![]() na slici 5.15 zaključujemo se na
dijelu grafa funkcije ista vrijednosti varijable
na slici 5.15 zaključujemo se na
dijelu grafa funkcije ista vrijednosti varijable ![]() javlja za tri
različite točke (konkretno, isti
javlja za tri
različite točke (konkretno, isti ![]() se javlja za po jedan
se javlja za po jedan ![]() iz
intervala
iz
intervala ![]() ,
, ![]() i
i
![]() ).
S druge strane, svakoj vrijednosti
).
S druge strane, svakoj vrijednosti
![]() odgovara točno
jedan
odgovara točno
jedan ![]() (funkcija
(funkcija ![]() je na tom intervalu injekcija).
Također, kako funkcija
je na tom intervalu injekcija).
Također, kako funkcija ![]() raste na intervalu
raste na intervalu ![]() , a pada na
intervalu
, a pada na
intervalu
![]() , zaključujemo da tu graf funkcije ima
petlju.
, zaključujemo da tu graf funkcije ima
petlju.
Iz tablice 5.1 se također lijepo vidi da graf krivulje ima
petlju za
![]() , odnosno za
, odnosno za
![]() , kao i
da svakoj vrijednosti
, kao i
da svakoj vrijednosti
![]() odgovaraju tri vrijednosti varijable
odgovaraju tri vrijednosti varijable ![]() .
.
Radi preglednosti rezultate ćemo
opet prikazati tablično. U tablici 5.2 dani su redom
intervali parametra ![]() , ponašanje derivacije
, ponašanje derivacije ![]() ,
ponašanje varijable
,
ponašanje varijable ![]() i konačan zaključak o zakrivljenosti.
i konačan zaključak o zakrivljenosti.