Kod ekstrema razlikujemo lokalne i globalne ekstreme. Za ispitivanje lokalnih ekstrema koristimo Fermatov teorem 5.6 i Teorem o monotonosti 5.11.
U definiciji lokalnih ekstrema te u iskazima i dokazima teorema o
ekstremima, koristimo pojam
![]() -okoline:
-okoline:
![]() -okolina točke
-okolina točke ![]() je interval
je interval
![]() pri čemu je
pri čemu je
![]() .
.
Razlike između lokalnih i globalnih ekstrema prikazane su na slici
5.9. Kod lokalnih ekstrema se traži da je vrijednost funkcije
u točki ekstrema strogo najmanja ili najveća na nekoj okolini.
S druge strane, definicija globalnih ekstrema dozvoljava da se
globalni ekstrem nalazi u više točaka pa čak i na nekom intervalu.
Na primjer, za prikazanu funkciju
![]() vrijedi sljedeće:
vrijedi sljedeće:
Za iskazivanje teorema koji daju uvjete za postojanje ekstrema, potrebna nam je sljedeća definicija.
Na primjer, za funkciju prikazanu na slici 5.9 stacionarne
točke su sve točke u intervalima ![]() i
i ![]() te točke
te točke ![]() ,
, ![]() i
i ![]() . Kritične točke su sve navedene točke te još točke
. Kritične točke su sve navedene točke te još točke
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() i
i ![]() .
.
Razlikujemo dvije vrste uvjeta za postojanje lokalnog ekstrema u nekoj točki: nužan uvjet je uvjet kojeg ispunjava svaka točka u kojoj funkcija ima lokalni ekstrem; dovoljan uvjet je uvjet koji znači da funkcija u nekoj točki ima lokalni ekstrem čim je taj uvjet ispunjen.
Na primjer, vidimo da su točke ![]() ,
, ![]() ,
, ![]() i
i ![]() u kojima funkcija
prikazana na slici 5.9 ima lokalne ekstreme
ujedno i kritične točke te funkcije.
S druge strane, vidimo da teorem 5.12 daje samo nužan, a ne i
dovoljan uvjet za postojanje lokalnog ekstrema, jer funkcija nema
lokalne ekstreme u ostalim kritičnim točkama.
u kojima funkcija
prikazana na slici 5.9 ima lokalne ekstreme
ujedno i kritične točke te funkcije.
S druge strane, vidimo da teorem 5.12 daje samo nužan, a ne i
dovoljan uvjet za postojanje lokalnog ekstrema, jer funkcija nema
lokalne ekstreme u ostalim kritičnim točkama.
Teorem 5.12 ćemo ilustrirati još jednim primjerom.
Za iskazivanje teorema koji daju dovoljne uvjete za postojanje ekstrema, potrebna nam je sljedeća definicija.
Primijetimo da funkcija može mijenjati predznak u nekoj točki, a da pri tome nije definirana u toj točki.
Na primjer, funkcije iz primjera 5.13 a) i b) ispunjavaju uvjete teorema, dok funkcija iz primjera 5.13 c) te uvjete ne ispunjava.
Dovoljan uvjet za postojanje ekstrema možemo izraziti i pomoću druge derivacije.
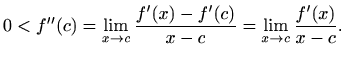
Zadnja jednakost vrijedi jer je
Prethodni dokaz možemo riječima iskazati i na sljedeći način:
ako je ![]() , tada je
, tada je ![]() veća od nule i na nekoj okolini točke
veća od nule i na nekoj okolini točke
![]() . To znači da je prva derivacija
. To znači da je prva derivacija ![]() strogo rastuća na toj
okolini. Kako je
strogo rastuća na toj
okolini. Kako je ![]() , zaključujemo da je
, zaključujemo da je ![]() negativna lijevo od
točke
negativna lijevo od
točke ![]() i pozitivna desno do točke
i pozitivna desno do točke ![]() . To pak znači da funkcija
. To pak znači da funkcija ![]() strogo pada lijevo od točke
strogo pada lijevo od točke ![]() , a strogo raste desno od točke
, a strogo raste desno od točke ![]() pa je
pa je
![]() točka lokalnog minimuma.
točka lokalnog minimuma.
Na primjer, funkcija ![]() ispunjava uvjete teorema 5.14 u
točki
ispunjava uvjete teorema 5.14 u
točki ![]() , jer je
, jer je ![]() , a
, a
![]() pa se u točki
pa se u točki
![]() nalazi lokalni minimum.
S druge strane, teorem ne možemo primijeniti na funkciju
nalazi lokalni minimum.
S druge strane, teorem ne možemo primijeniti na funkciju ![]() u točki
u točki ![]() , jer nije derivabilna u toj točki.
Teorem također ne možemo primijeniti niti na funkciju
, jer nije derivabilna u toj točki.
Teorem također ne možemo primijeniti niti na funkciju ![]() u
točki
u
točki ![]() , jer je
, jer je ![]() i
i ![]() . U tom slučaju možemo
koristiti više derivacije (vidi teorem 5.18).
. U tom slučaju možemo
koristiti više derivacije (vidi teorem 5.18).