Asimptota funkcije je pravac sa svojstvom da udaljenost između točke na grafu funkcije i tog pravca teži k nuli kada točka na grafu odmiče u beskonačnost. Funkcija može imati vertikalne, horizontalne i kose asimptote.
Pravac ![]() je vertikalna asimptota funkcije
je vertikalna asimptota funkcije ![]() u točki
u točki ![]() s lijeve strane
ako je
s lijeve strane
ako je
![]() ili
ili
![]() .
Analogno, pravac
.
Analogno, pravac ![]() je vertikalna asimptota funkcije
je vertikalna asimptota funkcije ![]() u
točki
u
točki ![]() s desne strane ako je
s desne strane ako je
![]() ili
ili
![]() .
Vertikalne asimptote se mogu nalaziti u
točkama prekida
funkcije ili u otvorenim rubovima područja definicije.
.
Vertikalne asimptote se mogu nalaziti u
točkama prekida
funkcije ili u otvorenim rubovima područja definicije.
Na primjer, pravac ![]() je vertikalna asimptota funkcije
je vertikalna asimptota funkcije
![]() s obje strane (slika 4.12).
Pravac
s obje strane (slika 4.12).
Pravac ![]() je vertikalna asimptota funkcija
je vertikalna asimptota funkcija ![]() ,
, ![]() i
i
![]() (slika 4.25) s desne strane.
U ovom slučaju vertikalna asimptota se nalazi u rubu područja
definicije.
(slika 4.25) s desne strane.
U ovom slučaju vertikalna asimptota se nalazi u rubu područja
definicije.
Pravac ![]() je horizontalna asimptota funkcije
je horizontalna asimptota funkcije ![]() u
lijevoj strani ako je
u
lijevoj strani ako je
![]() .
Analogno, pravac
.
Analogno, pravac ![]() je horizontalna asimptota funkcije
je horizontalna asimptota funkcije ![]() u
desnoj strani ako je
u
desnoj strani ako je
![]() .
Na primjer pravac
.
Na primjer pravac ![]() je horizontalna asimptota funkcije
je horizontalna asimptota funkcije
![]() u obje strane, kao i
u obje strane, kao i ![]() horizontalna asimptota
funkcija
horizontalna asimptota
funkcija ![]() i
i ![]() u lijevoj strani (slika 4.23).
u lijevoj strani (slika 4.23).
Ako je
tada je pravac
Izvedimo formule (4.5). Prema slici 4.16
udaljenost od točke na krivulji do asimptote je ![]() .
Prema definiciji asimptote
.
Prema definiciji asimptote
![]() kada
kada
![]() .
Kako je
.
Kako je
![]() konstanta, zaključujemo da
konstanta, zaključujemo da
Zadnji uvjet, koji je ekvivalentan s
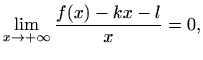
pa je
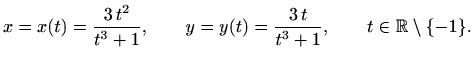
Kako su
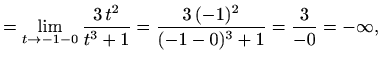 |
||
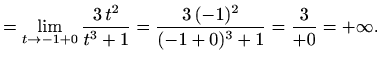 |
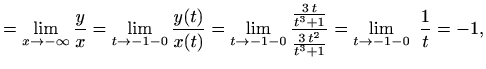 |
||
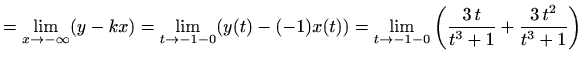 |
||
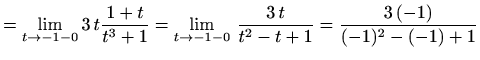 |
||