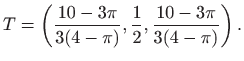U ovom poglavlju poopćit ćemo razmatranja iz poglavlja 2.6.7 na dvodimenzionalni i trodimenzionalni slučaj.
Promotrimo ravnu ploču
![]() gustoće
gustoće ![]() koja zauzima
područje
koja zauzima
područje
![]() .
Ploču ćemo podijeliti na male pravokutnike
.
Ploču ćemo podijeliti na male pravokutnike ![]() površine
površine
![]() . Označimo li središte
pravokutnika
. Označimo li središte
pravokutnika ![]() s
s
![]() , masa
, masa ![]() dotičnog
pravokutnika je približno jednaka
dotičnog
pravokutnika je približno jednaka
dok su momenti oko osi
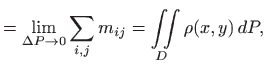 |
||
![$\displaystyle =\lim_{\Delta P \to 0}\sum_{i,j} [M_x]_{ij} = \iint\limits_D y \rho(x,y) dP,$](img2243.gif) |
||
![$\displaystyle =\lim_{\Delta P \to 0}\sum_{i,j} [M_y]_{ij} = \iint\limits_D x \rho(x,y) dP,$](img2245.gif) |
Koordinate težišta ploče
![]() su, kao i u poglavlju 2.6.7, jednake
su, kao i u poglavlju 2.6.7, jednake
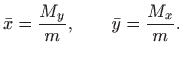
Prelaskom na polarne koordinate imamo
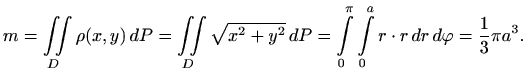
Nadalje, kako su i ploča i funkcija gustoće simetrične s obzirom na
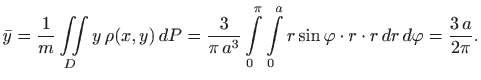
Dakle, težište se nalazi u točki
Moment inercije ili moment drugog reda
čestice mase ![]() oko
oko ![]() -osi definiramo kao
-osi definiramo kao ![]() , pri čemu je
, pri čemu je ![]() udaljenost čestice od osi. Kao i u prethodnom izlaganju, ploču
podijelimo na male pravokutnike, zbrojimo momente inercije oko
udaljenost čestice od osi. Kao i u prethodnom izlaganju, ploču
podijelimo na male pravokutnike, zbrojimo momente inercije oko ![]() -osi svih
pravokutnika te pređemo na limes kada površine pravokutnika teže nuli. Na
taj način dobili smo moment inercije ploče
-osi svih
pravokutnika te pređemo na limes kada površine pravokutnika teže nuli. Na
taj način dobili smo moment inercije ploče ![]() oko
oko ![]() -osi:
-osi:
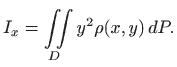
Slično dobijemo i izraz za moment moment inercije ploče
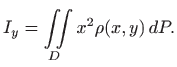
Moment inercije ploče
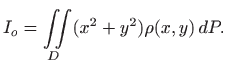
Primijetimo da je
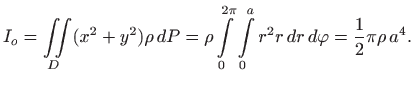
Zbog simetrije problema je
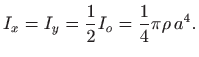
Uočimo da je masa diska jednaka
pa je
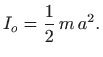
Dakle, ako povećamo radijus ili masu diska, povećat će se i moment inercije. Što je moment inercije veći, to je teže pokretanje i zaustavljanje rotacije diska oko osovine.
Promotrimo sada trodimenzionalni slučaj tijela ![]() gustoće
gustoće
![]() koje zauzima područje
koje zauzima područje
![]() . Sličnim razmatranjem kao i do sada masa
tijela
. Sličnim razmatranjem kao i do sada masa
tijela ![]() jednaka je
jednaka je
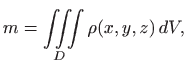
pri čemu je
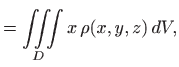 |
||
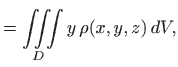 |
||
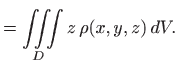 |
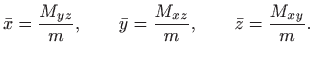
Momenti inercije oko koordinatnih osiju su
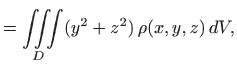 |
||
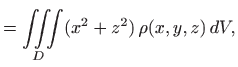 |
||
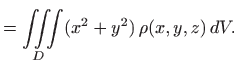 |
Tijelo zaprema područje
Masa tijela jednaka je
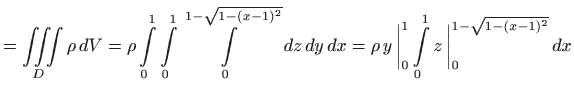 |
||
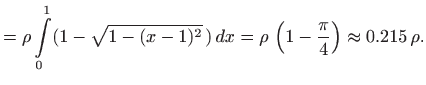 |
Vrijedi
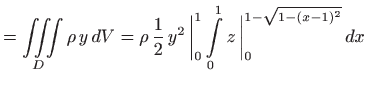 |
||
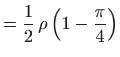 |
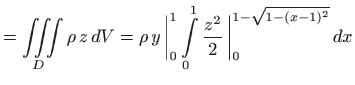 |
||
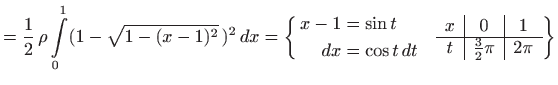 |
||
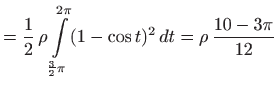 |
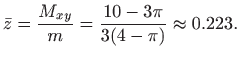
Zbog simetrije zaključujemo da vrijedi4.6