Pojam Richardsonova ekstrapolacija označava klasu metoda kojima se pomoću približnog računa s manje koraka postiže veća točnost. Kod numeričkog računanja integrala, Richardsonova ekstrapolacija je jednostavan način za ocjenu pogreške.
Metoda se sastoji u sljedećem:
ako smo numerički izračunali integral ![]() i integral
i integral ![]() koristeći dvostruko više točaka te ako se
u pripadnoj ocjeni ostatka javlja član
koristeći dvostruko više točaka te ako se
u pripadnoj ocjeni ostatka javlja član
![]() , onda je pogreška kod
računanja
, onda je pogreška kod
računanja ![]() približno manja od broja
približno manja od broja
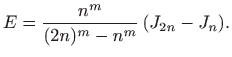
Drugim riječima, ako je
![$\displaystyle \int\limits _a^bf(x) dx\in[J_{2n},J_{2n}+E],
$](img1185.gif)
a ako je
![$\displaystyle \int\limits _a^bf(x) dx\in[J_{2n}+E,J_{2n}].
$](img1187.gif)
Kod dokazivanja ovih formula pretpostavljamo da postoji broj ![]() takav da je
takav da je
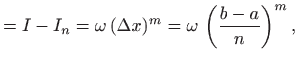 |
||
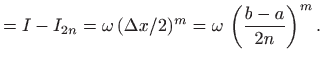 |
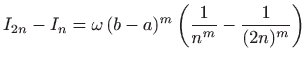
pa je
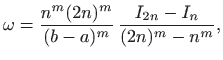
što konačno daje
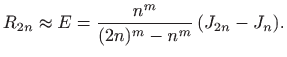
pa je
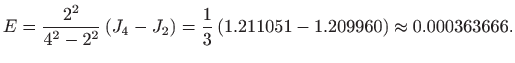
Dakle, za zadani integral (2.10) vrijedi
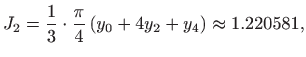
pa je
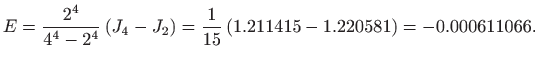
Dakle, za integral (2.10) vrijedi