 |
||
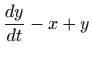 |
koje zadovoljava početne uvjete
 |
||
 |
Rješenje.
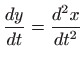 . Uvrštavanje
. Uvrštavanje
Konačno, uvrštavanje
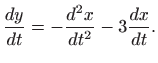
Uvrštavanjem
Uvrštavanje (5.10) i dobivenog rješenja
Iskoristimo sada zadane početne
uvjete. Iz uvjeta
![]() slijedi
slijedi ![]() , a iz uvjeta
, a iz uvjeta
![]() slijedi
slijedi
![]() . Dakle, rješenje diferencijalne jednadžbe koje
zadovoljava zadane dane početne uvjete je
. Dakle, rješenje diferencijalne jednadžbe koje
zadovoljava zadane dane početne uvjete je
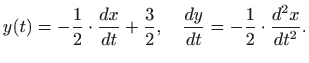
Uvrštavanjem u drugu jednadžbu sustava dobivamo linearnu nehomogenu diferencijalnu jednadžbu drugog reda s konstantnim koeficijentima
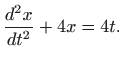
Rješenje pripadne homogene diferencijalne jednadžbe je
Uvrštavanjem dobivenog rješenja natrag u prvu jednadžbu sustava slijedi