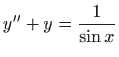 , te
provjerite linearnu nezavisnost rješenja pripadne homogene jednadžbe,
, te
provjerite linearnu nezavisnost rješenja pripadne homogene jednadžbe,
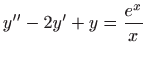 ,
,
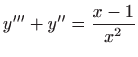 .
.
Metodom varijacije konstanti odredite opća rješenja diferencijalnih jednadžbi
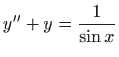 , te
provjerite linearnu nezavisnost rješenja pripadne homogene jednadžbe,
, te
provjerite linearnu nezavisnost rješenja pripadne homogene jednadžbe,
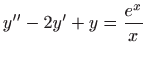 ,
,
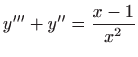 .
.
Rješenja.
pri čemu funkcije
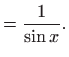 |
Množenje prve jednadžbe sa ![]() i druge jednadžbe s
i druge jednadžbe s ![]() te zbrajanje
jednadžbi daje
te zbrajanje
jednadžbi daje
![]() , pa je
, pa je
![]() .
.
U prethodnim formulama možemo uzeti ![]() i
i ![]() pa opće rješenje zadane
diferencijalne jednadžbe glasi
pa opće rješenje zadane
diferencijalne jednadžbe glasi
Linearnu nezavisnost rješenja homogene jednadžbe,
![]() i
i
![]() , provjerit ćemo računanjem determinante Wronskog prema
, provjerit ćemo računanjem determinante Wronskog prema
![]() [M2, poglavlje 5.10]:
[M2, poglavlje 5.10]:
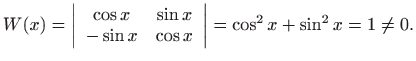 |
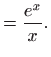 |
Stoga partikularno rješenje zadane diferencijalne jednadžbe ima oblik
pri čemu
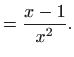 |
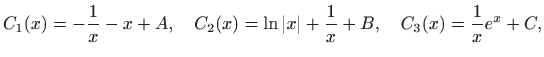
pa, uz