Red funkcija

U ovom poglavlju definirat ćemo red funkcija, konvergenciju u točki, te običnu, apsolutnu i uniformnu konvergenciju na nekom skupu. Pokazat ćemo kako se može odrediti područje konvergencije reda funkcija te dati jedan lako primjenjiv kriterij konvergencije.

Definicija 6.14 Red funkcija je zbroj beskonačno (prebrojivo mnogo) funkcija,

$\displaystyle % \sum_{n=1}^{\infty} f_n,$

pri čemu je $f_n:D\to \mathbb{R}$ . Koristimo i oznake

$\displaystyle % \sum_{n=1}^{\infty} f_n(x),\quad f_1+f_2+f_3+\cdots+f_n+\cdots .$

Funkcija

je -ti član reda, a funkcija

$\displaystyle % s_k=\sum_{n=1}^k f_n$

je -ta parcijalna suma. Niz funkcija $\{s_k\}$ je niz parcijalnih suma reda funkcija $\sum f_n$ .

Definicija 6.15

i): Red funkcija $\sum f_n$ konvergira u točki prema funkciji ako red realnih brojeva $\sum f_n(x)$ konvergira prema , odnosno ako niz realnih brojeva konvergira prema .
ii): Red funkcija $\sum f_n$ konvergira po točkama ili obično prema funkciji na skupu ako $\sum f_n(x)$ konvergira prema za $\forall x\in A$ , odnosno ako $s_k(x)\to s(x)$ za $\forall x\in A$ .
iii): Red funkcija $\sum f_n$ konvergira apsolutno na skupu ako red brojeva $\sum \vert f_n(x)\vert$ konvergira za $\forall x\in A$ .
iv): Red funkcija $\sum f_n$ konvergira uniformno prema funkciji na skupu ako niz funkcija $\{s_k\}$ konvergira uniformno prema funkciji na skupu .

Dakle, konvergenciju u nekoj točki i običnu konvergenciju možemo definirati na dva načina: preko reda brojeva ili preko niza parcijalnih suma. Također, pored obične konvergencije imamo još dvije različite vrste konvergencije, apsolutnu i uniformnu.

Primjer 6.15 Iz svojstava geometrijskog reda iz primjera 6.8 slijedi da za geometrijski red funkcija vrijedi

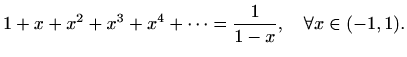
$\displaystyle % 1+x+x^2+x^3+x^4+\cdots =\frac{1}{1-x},\quad \forall x\in(-1,1).$

Konvergencija je apsolutna jer red $\sum \vert x\vert^{n-1}$ konvergira za $\forall x\in(-1,1)$ . Konvergencija je također uniformna prema teoremu 6.16, a prikazana je na slici 6.3. Također možete pogledati i animaciju konvergencije.

**Slika 6.3:** Konvergencija geometrijskog reda funkcija
$\begin{figure}\begin{center} \epsfig{file=slike/redfg.eps,width=10.2cm} \end{center}\end{figure}$

Poglavlja

Niz funkcija NIZOVI I REDOVI Ispitivanje konvergencije