×   HOME PREDAVANJA

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI INDEKS

VJEŽBE

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

KVIZ

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

PODSJETNIK

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

JAVA NETPLOT OCTAVE Traži ...

☰   matematika1 Red funkcija     Red funkcija     Red potencija

Ispitivanje konvergencije

Ispitati konvergenciju reda funkcija znači naći područje, odnosno sve vrijednosti $x$ , za koje dani red konvergira. Često ispitujemo područje apsolutne konvergencije koristeći kriterije konvergencije za redove realnih brojeva iz poglavlja 6.2.2. Postupak ćemo objasniti na primjeru.

Zadan je red funkcija

$$\sum_{n=1}^{\infty} \frac{x^{n-1}}{(1-x)^n}.$$ (6.5)

Cauchyjev kriterij iz teorema 6.10 daje

$$% \lim_{n\to \infty} \sqrt[n]{\vert f_n(x)\vert} = \lim_{n\to \i... ...t x\vert^{\frac{n-1}{n}}}{\vert 1-x\vert}= \left\vert\frac{x}{1-x}\right\vert.$$

Dakle, red (6.5) konvergira apsolutno za sve točke $x\in \mathbb{R}\setminus\{1\}$ za koje je

$$% \left\vert\frac{x}{1-x}\right\vert<1,$$

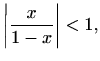
odnosno za $x\in (-\infty,1/2)$ . U točki $x=1/2$ Cauchyjev kriterij ne daje odluku pa ćemo taj slučaj razmotriti posebno:

$$\sum f_n\left(\frac{1}{2}\right) =\sum \frac{\left(\frac{1}{2}\right)^{n-1}} {\left(\frac{1}{2}\right)^{n}} =\sum 2=+\infty.$$

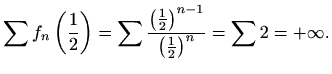
Uniformnu konvergenciju možemo ispitati na sljedeći način.

Teorem 6.15   [Weierstrass] Red funkcija $\sum f_n$ , pri čemu je $f_n:D\to \mathbb{R}$ , konvergira uniformno na skupu $D$ ako ima konvergentnu majorantu $\sum a_n$ , $a_n\in \mathbb{R}$ , odnosno

$$(\exists n_0\in \mathbb{N}) \textrm{ takav da } n\geq n_0 \Rightarrow \vert f_n(x)\vert\leq a_n, \forall x\in D.$$