×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Primjeri     Varijacijski račun     Eulerova metoda konačnih razlika

Uvjetni ekstrem

Postupak traženja uvjetnih (ili vezanih) ekstrema funkcionala je vrlo sličan postupku traženja uvjetnih ekstrema funkcija više varijabla, odnosno koristi se metoda Lagrangeovih multiplikatora (vidi poglavlje 3.12).

Zadatak je naći funkcije $x_1(t),\ldots,x_n(t)$ koje su ekstremi funkcionala

$$I(x_1,\ldots, x_n)=\int\limits _a^b F(t,x_1,\ldots, x_n, x'_1,\ldots, x'_n) dt,$$

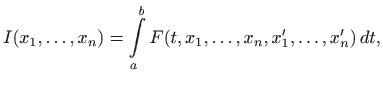
a istovremeno zadovoljavaju rubne uvjete

$$x_i(a)=A_i, \qquad x_i(b)=B_i, \qquad A_i,B_i\in\mathbb{R}, \qquad i=1,\ldots,n,$$

i ograničenja (uvjete) koja mogu biti algebarske jednadžbe,

$$h_k(t,x_1,\ldots,x_n)=0, \qquad k=1,\ldots,m, \quad m<n,$$

diferencijalne jednadžbe,

$$h_k(t, x_1,\ldots,x_n, x'_1,\ldots, x'_n)=0, \qquad k=1,\ldots,m, \quad m<n,$$

ili takozvana izoperimetrička ograničenja,

$$\int\limits _a^b h_k(t,x_1,\ldots,x_n, x'_1,\ldots, x'_n)=0, \qquad L_k\in \mathbb{R}, \quad k=1,\ldots m.$$

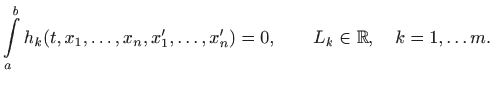
Zadatak se rješava na sljedeći način: prvo se formira pomoćni funkcional

$$I^*=\int\limits _a^b F^* dt\equiv \int\limits _a^b \left[ F(t, x_1,\ldots, x_n, x'_1,\ldots, x'_n) +\sum \lambda_k(t) h_k \right] dt$$

pri čemu su Lagrangeovi multiplikatori $\lambda_k$ funkcije od $t$ , a potom se rješenje polaznog problema dobije iz sustava od $n$ Euler-Lagrangeovih jednadžbi

$$\frac{\partial F^*}{\partial x_i}-\frac{d}{dt} \frac{\partial F^*}{\partial x'_i}=0,\qquad i=1,\ldots,n,$$

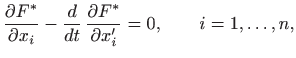
rubnih uvjeta i zadanih ograničenja.

Primjer 4.25   Nađimo ekstrem funkcionala

$$I(y,z)=\int\limits _0^a \sqrt{\frac{1+y'z'}{x}} dx, \qquad y(0)=0,\quad y(a)=b,\quad y=z+1.$$

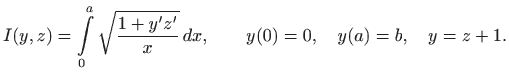
Pomoćni funkcional glasi

$$I^*=\int\limits _0^a \left[ \sqrt{\frac{1+y'z'}{x}} + \lambda(x) (y-z-1)\right] dx.$$

Iz uvjeta $y=z+1$ vidimo da su zadana sva četiri rubna uvjeta:

$$y(0)=0,\quad y(a)=b,\quad z(0)=-1,\quad z(a)=b-1.$$

Rješenje dobijemo iz Euler-Lagrangeovih jednadžbi

$$\frac{\partial F^*}{\partial y}-\frac{d}{dx} \frac{\partial F^*}{\partial y'} = \lambda(x)-\frac{d}{dx} \left( \frac{z'}{2 \sqrt{x (1+y'z')}}\right)=0,$$

$$\frac{\partial F^*}{\partial z}-\frac{d}{dx} \frac{\partial F^*}{\partial z'} = -\lambda(x)-\frac{d}{dx} \left( \frac{y'}{2 \sqrt{x (1+y'z')}}\right)=0,$$

rubnih uvjeta i ograničenja $y=z+1$ . Zbrajanjem jednadžbi imamo

$$\frac{d}{dx} \left( \frac{y'+z'}{2 \sqrt{x (1+y'z')}}\right)=0.$$

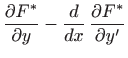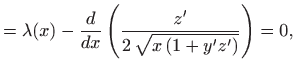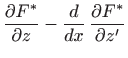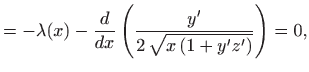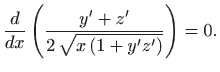
Zadano ograničenje povlači $y'=z'$ pa prethodna jednadžba prelazi u

$$\frac{d}{dx} \left( \frac{y'}{\sqrt{x (1+y^{\prime 2})}}\right)=0.$$

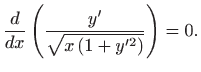
Dakle, $y$ je cikloida (vidi primjer 4.22) dok je $z=y-1$ .

Primjer 4.26   Nađimo ekstrem funkcionala

$$I(x)=\int\limits _0^1 (x'')^2 dt, \qquad x(0)=1, x(1)=0, x'(0)=1, x'(1)=0.$$

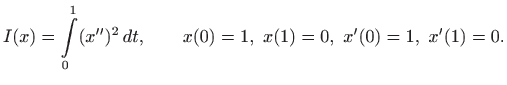
U podintegralnoj funkciji javlja se druga derivacija funkcije $x(t)$ , što je potrebno eliminirati. Uvedimo nove funkcije

$$x_1(t)=x(t),\qquad x_2(t)=x'_1(t).$$

Zadani problem prelazi u ekvivalentni problem

$$I(x_1,x_2)=\int\limits _0^1 (x'_2)^2 dt, \qquad x_1(0)=1, x_1(1)=0, x_2(0)=1, x_2(1)=0,$$

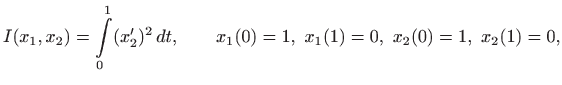
uz ograničenje $x_2-x'_1=0$ . Pomoćni funkcional glasi

$$I^*=\int\limits _0^1 \left[ (x'_2)^2 +\lambda(t) (x_2-x'_1)\right] dt.$$

Euler-Lagrangeove jednadžbe glase

$$\frac{\partial F^*}{\partial x_1}-\frac{d}{dt} \frac{\partial F^*}{\partial x'_1} = 0-\frac{d}{dt} (-\lambda(t))=0,$$

$$\frac{\partial F^*}{\partial x_2}-\frac{d}{dt} \frac{\partial F^*}{\partial x'_2} = \lambda(t)-\frac{d}{dt}(x'_2(t))=0.$$

Iz prve jednadžbe slijedi $\lambda'(t)=0$ , a iz druge $\lambda(t)=x''_2(t)$ . Deriviranje zadnje jednadžbe daje

$$\lambda'(t)=x'''_2(t)=0$$

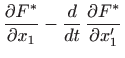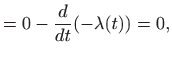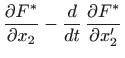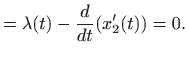pa je

$$x_2(t)=a t^2 + b t + c$$

za neke konstante $a$ , $b$ i $c$ . Ograničenje $x'_1=x_2$ povlači

$$x_1(t)=a \frac{t^3}{3}+b \frac{t^2}{2} + c t+d$$

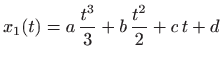
za neku konstantu $d$ . Rubni uvjeti daju

$$x_1(0)=1=d,\qquad x_2(0)=1=c.$$

Nadalje, vrijedi

$$x_1(1)=0=\frac{a}{3}+\frac{b}{2}+1,\qquad x_2(1)=0=a+b+1,$$

pa je $a=3$ i $b=-4$ . Dakle, rješenje je dano s

$$x_1(t)=t^3-2 t^2+t+1,\qquad x_2(t)=3 t^2-4 t+1,$$

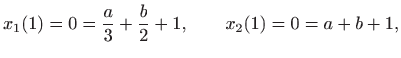
pa je tražena vrijednost zadanog funkcionala jednaka

$$I=\int\limits _0^1 (6 t-4)^2 dt= 4.$$

Primjer 4.27   Nađimo ekstrem funkcionala

$$I(y,z)=\int\limits _0^1 (y^{\prime 2} + z^{\prime 2} -4 x z'-4 z) dx,$$

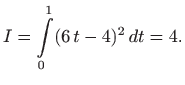
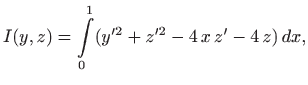
uz rubne uvjete

$$y(0)=0,\quad z(0)=0,\quad y(1)=1,\quad z(1)=1,$$

i uz izoperimetričko ograničenje

$$\int\limits _0^1 ( y^{\prime 2} -x y'- z^{\prime 2}) dx=2.$$

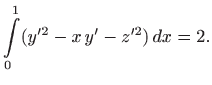
Pomoćni funkcional glasi

$$I^*=\int\limits _0^1 \left[ y^{\prime 2} + z^{\prime 2} -4 x z'-4 z +\lambda (y^{\prime 2} -x y'- z^{\prime 2}) \right] dx.$$

Euler-Lagrangeove jednadžbe glase

$$\frac{\partial F^*}{\partial y}-\frac{d}{dx} \frac{\partial F^*}{\partial y'} = 0-\frac{d}{dx}(2 y'+2 y'\lambda -\lambda x)=0,$$

$$\frac{\partial F^*}{\partial z}-\frac{d}{dx} \frac{\partial F^*}{\partial z'} = -4 - \frac{d}{dx}(2 z'-4 x -2 \lambda z')=0.$$ (4.8)

Integriranje prve jednadžbe daje

$$2 y'+2 y'\lambda -\lambda x =a,$$

odnosno

$$y'=\frac{\lambda x+a}{2+2 \lambda}$$

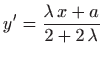
pa ponovno integriranje daje

$$y=\frac{\lambda \frac{x^2}{2} +a x}{2+2 \lambda}+b$$

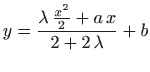
za neke konstante $a$ i $b$ . Rubni uvjet $y(0)=0$ povlači $b=0$ , a rubni uvjet $y(1)=1$ povlači $a=2+\frac{3}{2} \lambda$ pa je

$$y(x)=\frac{\lambda x^2 + (3 \lambda +4) x}{4+4 \lambda}.$$

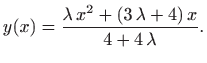
Integriranje jednadžbe (4.8) daje

$$2 z'-4 x -2 \lambda z'=-4 x + c,$$

odnosno

$$z'=\frac{c}{2-2 \lambda}$$

pa ponovno integriranje daje

$$z= \frac{c}{2-2 \lambda} x+d$$

za konstante $c$ i $d$ . Rubni uvjet $z(0)=0$ povlači $d=0$ , a rubni uvjet $z(1)=1$ povlači $c=2-2 \lambda$ pa je

$$z(x)=x.$$

Konačno, uvrštavanjem izraza za $y$ , $y'$ , $z$ i $z'$ u zadano izoperimetričko ograničenje, dobijemo da je $\lambda =-11/10$ . Dovršite ovaj račun za vježbu!

Primjeri     Varijacijski račun     Eulerova metoda konačnih razlika