Točke lokalnih minimuma i točke lokalnih maksimuma funkcije ![]() zajedničkim imenom zovemo točkama
lokalnih ekstrema
funkcije
zajedničkim imenom zovemo točkama
lokalnih ekstrema
funkcije ![]() .
Kao i kod funkcija jedne varijable, ukoliko je funkcija
.
Kao i kod funkcija jedne varijable, ukoliko je funkcija ![]() više
varijabla neprekidna te barem dvaput derivabilna u nekoj okolini
promatrane točke
više
varijabla neprekidna te barem dvaput derivabilna u nekoj okolini
promatrane točke ![]() , možemo dati nužne i dovoljne uvjete da bi
, možemo dati nužne i dovoljne uvjete da bi ![]() imala lokalni ekstrem u
imala lokalni ekstrem u ![]() izražene pomoću vrijednosti parcijalnih
derivacija od
izražene pomoću vrijednosti parcijalnih
derivacija od ![]() u promatranoj točki. Ti su uvjeti analogni onima za
funkcije jedne varijable, ali dakako nešto složenije izraženi.
u promatranoj točki. Ti su uvjeti analogni onima za
funkcije jedne varijable, ali dakako nešto složenije izraženi.
gdje je
Nužan uvjet ekstrema funkcije jedne varijable povlači
može iskazati pomoću diferencijala kao
Kao što ćemo vidjeti, ovaj uvjet je nužan, ali ne i dovoljan. Ako je funkcija
jer je ta funkcija beskonačno puta diferencijabilna s parcijalnim derivacijama prvog reda
i očito je
Jednadžba tangencijalne ravnine na plohu
je beskonačno puta diferencijabilna, a parcijalne derivacije prvog reda su joj
Očito je
ali isto tako i točke oblika
Stoga zaključujemo da
ima u točki
Međutim točku
Kako smo vidjeli u gornjem primjeru, stacionarnost neke točke nije
dovoljan uvjet da bi ta točka bila točka lokalnog ekstrema.
Da bismo mogli dati primjenjive dovoljne uvjete moramo, kao i u slučaju
funkcija jedne varijable, koristiti derivacije viših redova. Iz
definicije 3.11 vidljivo je da je ![]() točka lokalnog ekstrema
funkcije
točka lokalnog ekstrema
funkcije ![]() ako i samo ako je razlika
ako i samo ako je razlika
![]() stalnog predznaka
u nekoj okolini
stalnog predznaka
u nekoj okolini
![]() točke
točke ![]() .
Za ocjenu predznaka te razlike najprikladnije je upotrijebiti
Taylorovu formulu
iz teorema 3.6 za
.
Za ocjenu predznaka te razlike najprikladnije je upotrijebiti
Taylorovu formulu
iz teorema 3.6 za ![]() , što znači
korištenje parcijalnih derivacija od
, što znači
korištenje parcijalnih derivacija od ![]() do uključivo drugog reda. Formula se
dodatno pojednostavnjuje uvažavanjem nužnog uvjeta
do uključivo drugog reda. Formula se
dodatno pojednostavnjuje uvažavanjem nužnog uvjeta ![]() .
.
Dakle, uz pretpostavku da je ![]() funkcija
od
funkcija
od ![]() varijabla koja u nekoj okolini
varijabla koja u nekoj okolini
![]() stacionarne točke
stacionarne točke
![]() ima neprekidne parcijalne
derivacije do uključivo drugog reda, primjenom Taylorove formule s
Lagrangeovim oblikom ostatka
ima neprekidne parcijalne
derivacije do uključivo drugog reda, primjenom Taylorove formule s
Lagrangeovim oblikom ostatka ![]() dobivamo da
za svaku točku
dobivamo da
za svaku točku
![]() vrijedi
vrijedi
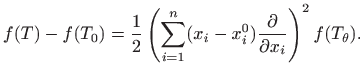
U daljnjoj analizi ključno je uočiti da se, zbog pretpostavljene neprekidnosti svih parcijalnih derivacija drugog reda funkcije
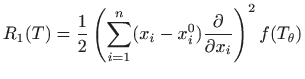
i veličina
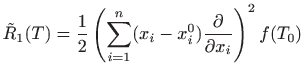
vrlo malo razlikuju čim je točka
Nastupanje bilo kojeg od gore navedenih četiriju slučajeva
zavisi isključivo o vrijednostima parcijalnih derivacija drugog reda
funkcije ![]() u promatranoj točki
u promatranoj točki ![]() .
Vrijedi sljedeći teorem:
.
Vrijedi sljedeći teorem:
Za
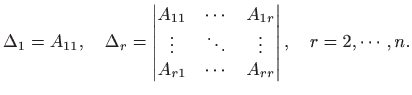
Tada vrijedi:
Dakle,
pa se tvrdnje teorema 3.8 svode na sljedeća četiri slučaja:
jedina stacionarna točka je
pa u točki
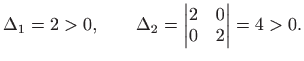
Prema teoremu 3.8 a) funkcija
jedina stacionarna točka je
pa u točki
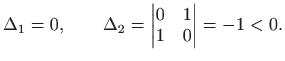
Prema teoremu 3.8 c) funkcija
ima lokalni maksimum u točki
je beskonačno puta diferencijabilna, a parcijalne derivacije prvog reda su
Očito je
pa u točki
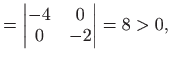 |
||
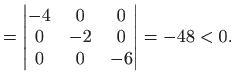 |
je beskonačno puta diferencijabilna, a parcijalne derivacije prvog reda su joj
Opet je
U točki
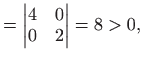 |
||
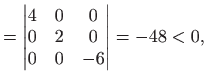 |
Nadalje, točka
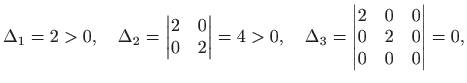
odnosno radi se o slučaju d) teorema 3.8.