Promatrimo funkciju
![]() ,
,
![]() ,
i točke
,
i točke
iz
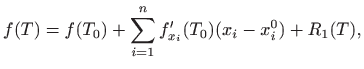
pri čemu ostatak
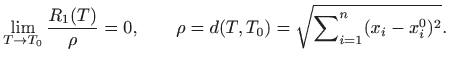
Praktična korist od gornje interpretacije je sljedeći zaključak: ako je
točka ![]() blizu točki
blizu točki ![]() , odnosno ako je
, odnosno ako je ![]() malen, onda je veličina
malen, onda je veličina
![]() zanemarivo malena pa se vrijednost funkcije
zanemarivo malena pa se vrijednost funkcije ![]() u točki
u točki ![]() može računati
korištenjem približne jednakosti
može računati
korištenjem približne jednakosti
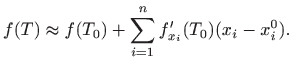
Desnu stranu u gornjoj približnoj jednakosti je jednostavno računati ako su poznate vrijednosti
Koristeći Taylorovu formulu za realne funkcije jedne varijable te formulu za deriviranje kompozicije funkcija više varijabla lako se dobije Taylorova formula za funkcije više varijabla. Taj rezultat ovdje iskazujemo bez dokaza:
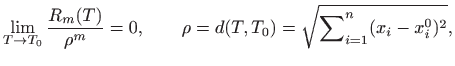
što se u literaturi (naročito u numeričkoj analizi) simbolički zapisuje kao
(ovakav zapis zovemo Peannov oblik ostatka). Posebno za
onda graničnim prijelazom iz Taylorove formule dobivamo razvoj funkcije u Taylorov red oko točke
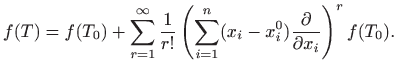
U slučaju kad je
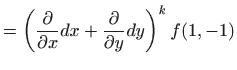 |
||
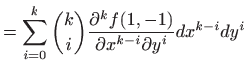 |
||
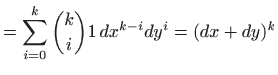 |
||
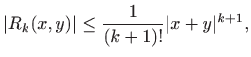
pa je
U ovom slučaju smo red (3.2) mogli dobiti i direktno iz Maclaurinovog razvoja
funkcije jedne varijable
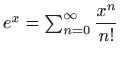 koji konvergira za svaki
koji konvergira za svaki
![]() pomoću formalne zamjene
pomoću formalne zamjene ![]() .
.