Ako je funkcija jedne varijable
![]() ,
,
![]() ,
derivabilna (dakle diferencijabilna) u točki
,
derivabilna (dakle diferencijabilna) u točki ![]() , onda je
pravac
, onda je
pravac ![]() zadan jednadžbom
zadan jednadžbom
tangenta krivulje
Slično možemo postupiti kad imamo funkciju dviju varijabla.
Neka je
![]() ,
,
![]() .
Ako je
.
Ako je ![]() diferencijabilna u točki
diferencijabilna u točki
![]() , onda postoje parcijalne derivacije
, onda postoje parcijalne derivacije
![]() i
i
![]() te možemo definirati dva pravca
te možemo definirati dva pravca ![]() i
i ![]() u
prostoru koji prolaze točkom
u
prostoru koji prolaze točkom
![]() , gdje je
, gdje je
![]() :
:
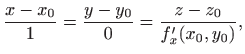 |
||
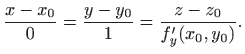 |
Pravci ![]() i
i ![]() imaju vektore smjerova
imaju vektore smjerova
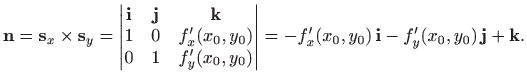
Prema tome,
je jednadžba tangencijalne ravnina na plohu
možemo interpretirati kao prirast varijable
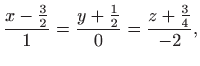 |
||
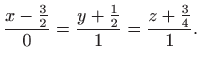 |
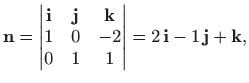
a jednadžba tangencijalne ravnine glasi (vidi sliku 3.26)
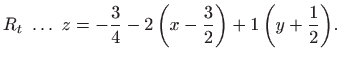
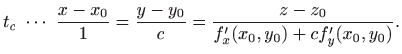
S druge strane, presjek plohe
pri čemu se sve nalazi u ravnini
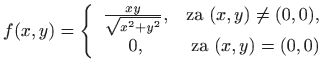
u točki
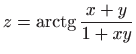
u točki
Za crtanje ploha i normala na plohe možete koristiti java aplet.