U Matematici 1 smo već govorili o tome kako jednadžbu oblika
gdje je
Jednadžbi
i u pravilu ga poistovjećujemo sa samom jednadžbom kojoj je pridružen.
Ova definicija zahtijeva dva komentara koja dajemo u sljedeće dvije napomene, zajedno s jednostavnim primjerima
onda je možemo shvatiti i kao funkciju koja je implicitno zadana jednadžbom
pri čemu je domena od
je implicitna jednadžbom kružnice sa središtem u ishodištu
odnosno
Međutim, i funkcija
![$\displaystyle f(x)=\left\{\begin{array}{rl}\sqrt{1-x^2},&\textrm{za } x\in [-1,0.5)\\
-\sqrt{1-x^2},&\textrm{za } x\in [0.5,1]\end{array}\right.
$](img1784.gif)
prikazana na slici 3.31) je također implicitno zadana jednadžbom
često interpretiramo kao jednadžbu pravca u ravnini koji prolazi točkom
obično nazivamo implicitnom jednadžbom parabole. Tu je
S druge strane pogodnije je varijablu ![]() interpretirati kao
nezavisnu jer se onda
interpretirati kao
nezavisnu jer se onda ![]() može interpretirati kao jednadžba kojom je
implicitno zadana jedna osnovna funkcija
može interpretirati kao jednadžba kojom je
implicitno zadana jedna osnovna funkcija
čiji graf se podudara sa skupom
Definiciju 3.12 na prirodan način poopćavamo na slučaj više varijabla.
uvijek promatramo kao jednadžbu kojom može biti implicitno zadano više funkcija od
implicitno su zadana dva kružna stošca, oba s vrhom u ishodištu
Ovdje je funkcija
![]() definirana na skupu
definirana na skupu
![]() pa ako
varijablu
pa ako
varijablu ![]() tretiramo kao zavisnu, onda su gornjom jednadžbom
implicitno zadane dvije osnovne funkcije dviju nezavisnih varijabla
tretiramo kao zavisnu, onda su gornjom jednadžbom
implicitno zadane dvije osnovne funkcije dviju nezavisnih varijabla
![]() i
i ![]() :
:
Ako bi u gornjoj jednadžbi varijablu
i
Grafovi ovih funkcija su na slici 3.33.
je funkcija
Ova jednadžba se može ekvivalentno zapisati kao
što je jednadžba kružnog paraboloida s vrhom u točki
Zanima nas koji su
dovoljni uvjeti da bi formulom
![]() bila implicitno
zadana funkcija
bila implicitno
zadana funkcija ![]() takva da je
takva da je
i koja su svojstva tako zadane funkcije? Odgovore daje sljedeći teorem.
Tada vrijedi sljedeće:
i vrijedi
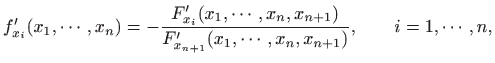
pri čemu je
definiranu pomoću funkcije
postojati okolina
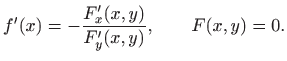
definirane pomoću funkcije
postojati okolina
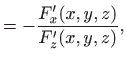 |
||
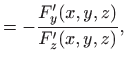 |
||
implicitno zadane dvije osnovne funkcije nezavisne varijable
Ovdje je
U točki
Pretpostavke teorema 3.9 ispunjene su i zato mora postojati okolina
Da bi izračunali na primjer
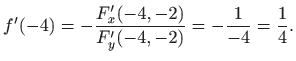
U ovom slučaju gornji račun možemo provjeriti koristeći eksplicitni izraz
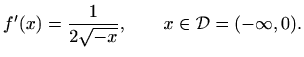
Jasno je da, općenito, takvu provjeru nećemo moći napraviti jer funkciju
kao implicitnu vezu triju varijabla. Zbog očite simetrije svejedno je koju varijablu tretiramo kao zavisnu pa uzmimo da je to varijabla
i u svim točkama
imamo
Prema tome, teorem 3.9 možemo primijeniti u svakoj točki
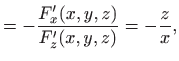 |
||
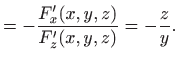 |
Krivulja
Stoga jednadžba ![]() ima točno jedno rješenje
ima točno jedno rješenje ![]() . Veličinu
. Veličinu
![]() ne možemo egzaktno izraziti koristeći elementarne funkcije jedne
varijable, već samo možemo upotrijebiti neku od elementarnih numeričkih
metoda (na primjer metodu bisekcije - za računanje možete koristiti i
ogovarajući java aplet)
da bi dobili približnu vrijednost od
ne možemo egzaktno izraziti koristeći elementarne funkcije jedne
varijable, već samo možemo upotrijebiti neku od elementarnih numeričkih
metoda (na primjer metodu bisekcije - za računanje možete koristiti i
ogovarajući java aplet)
da bi dobili približnu vrijednost od ![]() (vrijedi
(vrijedi
![]() ).
Zaključujemo da je početna jednadžba ekvivalentna s jednadžbom
).
Zaključujemo da je početna jednadžba ekvivalentna s jednadžbom
iz koje dobivamo eksplicitno varijablu
Sada neposrednim deriviranjem dobijamo