×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Teoremi o određenom integralu     ODREĐENI INTEGRAL     Kriteriji konvergencije

Nepravi integral

Nepravi integral je poopćenje određenog integrala kada područje integracije ima barem jednu beskonačnu granicu ili kada funkcija unutar područja integracije nije omeđena (na primjer, ima vertikalnu asimptotu). Neprave integrale rješavamo pomoću limesa. Ako je nepravi integral konačan, kažemo da je konvergentan ili da konvergira, u protivnom je divergentan, odnosno divergira.

Želimo, na primjer, odrediti površinu između krivulje $y=e^{-x}$ i $x$ -osi od nula do beskonačno (slika 2.8).

Slika 2.8: Nepravi integral

Lako se možemo uvjeriti da je tražena površina konačna, unatoč tome što se područje proteže u beskonačno. Naime, tražena površina je manja od sume površina pravokutnika označenih na slici 2.9. Ta je suma gornja integralna suma za $x_i=i$ , $i=0,1,\infty$ i $M_i=e^{-(n-1)}$ , a jednaka je sumi geometrijskog reda

$$\sum_{n=1}^{\infty} e^{-(n-1)}=\displaystyle \frac{1}{1-\displaystyle \frac{1}{e}}< 2.$$

Slika 2.9: Konvergentna gornja suma nepravog integrala

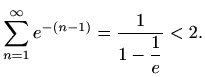
Površinu računamo pomoću nepravog integrala:

$$\int\limits _0^{+\infty} e^{-x} dx= \lim_{a\to +\infty} \int\... ...to +\infty} (-e^{-x} ) \bigg\vert _0^a = \lim_{a\to +\infty} -e^{-a} +e^0= 1.$$

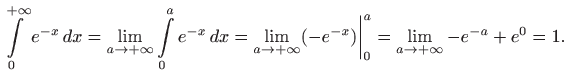
Sljedeći nepravi integral ponaša se kao red brojeva $\sum 1/n^p$ koji konvergira za $p>1$ , a divergira za $p\leq 1$ (vidi M1, poglavlje 6.2.2).

Primjer 2.3   Izračunajmo integral

$$I=\int\limits _1^{+\infty} \frac{1}{x^p} dx.$$

Prelaskom na limes imamo

$$I=\lim_{a\to +\infty} \int\limits _1^{a} x^{-p} dx.$$

Slučajeve $p=1$ , $p<1$ i $p>1$ analizirati ćemo posebno. Za $p=1$ vrijedi

$$I=\lim_{a\to +\infty} \ln \vert x\vert \bigg\vert _1^a = \lim_{a\to +\infty} \ln a - \ln 1= +\infty$$

pa integral divergira. Za $p\neq 1$ vrijedi

$$I=\lim_{a\to +\infty} \frac{1}{-p+1} x^{-p+1} \bigg\vert _1^a = \lim_{a\to +\infty} \frac{1}{1-p} a^{1-p} -\frac{1}{1-p}.$$

Za $p<1$ je $1-p>0$ , pa je $I=+\infty$ , odnosno integral divergira. Za $p>1$ je $1-p<0$ , pa je $I=1/(p-1)$ , odnosno integral konvergira.

Kao primjer nepravog integrala koji u rubu područja integracije ima vertikalnu asimptotu, uzet ćemo istu podintegralnu funkciju kao u prethodnom primjeru. Ponašanje integrala u odnosu vrijednost parametra $p$ obrnuto je nego u prethodnom primjeru.

Primjer 2.4   Izračunajmo integral

$$I=\int\limits _0^{1} \frac{1}{x^p} dx.$$

Prelaskom na limes imamo

$$I=\lim_{\varepsilon \to 0_+} \int\limits _{\varepsilon }^{1} x^{-p} dx.$$

Slučajeve $p=1$ , $p<1$ i $p>1$ analizirati ćemo posebno. Za $p=1$ vrijedi

$$I=\lim_{\varepsilon \to 0_+} \ln \vert x\vert \bigg\vert _{\varep... ... }^1 = \lim_{\varepsilon \to 0_+} \ln 1 - \ln \varepsilon = -(-\infty)=\infty$$

pa integral divergira. Za $p\neq 1$ vrijedi

$$I=\lim_{\varepsilon \to 0_+} \frac{1}{-p+1} x^{-p+1} \bigg\ver... ...1 = \lim_{\varepsilon \to 0_+} \frac{1}{1-p}-\frac{1}{1-p} \varepsilon ^{1-p}.$$

Za $p<1$ je $1-p>0$ , pa je $I=1/(1-p)$ , odnosno integral konvergira. Za $p>1$ je $1-p<0$ , pa je $I=+\infty$ , odnosno integral divergira.

U slučaju kada u nepravom integralu imamo i beskonačne granice i točke prekida, integral rastavljamo na više dijelova. Na primjer,

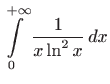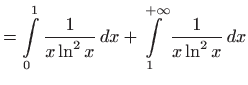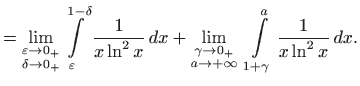$$\int\limits _0^{+\infty}\frac{1}{x\ln^2 x} dx = \int\limits _0^{1}\frac{1}{x\ln^2 x} dx+ \int\limits _1^{+\infty}\frac{1}{x\ln^2 x} dx$$

$$= \lim_{\substack{\varepsilon \to 0_+ \delta\to 0_+}} \int\lim... ...\to 0_+ a\to +\infty}} \int\limits _{1+\gamma}^{a}\frac{1}{x\ln^2 x} dx.$$

Zadatak 2.2   Riješite prethodni integral i pokažite da divergira u $+\infty$ .

Poglavlja

• Kriteriji konvergencije

Teoremi o određenom integralu     ODREĐENI INTEGRAL     Kriteriji konvergencije