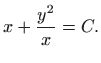| (5.4) |
Diferencijalna jednadžba oblika
Opišimo postupak nalaženja funkcije ![]() . Ukoliko navedena funkcija
. Ukoliko navedena funkcija ![]() postoji, onda je
postoji, onda je
![]() , odnosno
, odnosno
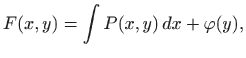
pri čemu je
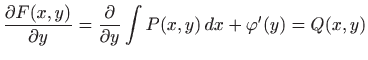
pa je
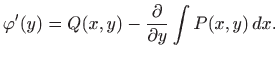
Izraz na desnoj strani prethodne jednakosti je funkcija od
![$\displaystyle \frac{\partial}{\partial x}\left[Q(x,y)-\frac{\partial}{\partial y} \int P(x,y) dx\right]$](img2944.gif) |
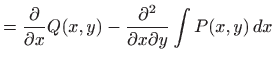 |
|
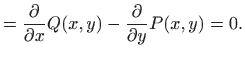 |
![$\displaystyle \varphi (y)=\int \left[ Q(x,y) dy- \frac{\partial}{\partial y} \int P(x,y) dx\right]
dy
$](img2947.gif)
pa je konačno
![$\displaystyle F(x,y)=\int P(x,y) dx+\int \left[ Q(x,y) dy- \frac{\partial}{\partial y}
\int P(x,y) dx\right] dy.
$](img2948.gif)
Kako je
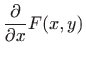 |
||
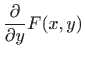 |
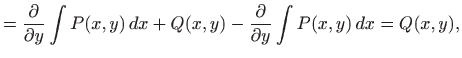 |
Za neke jednadžbe oblika (5.4) koje nisu egzaktne, postoji
funkcija ![]() takva da je jednadžba
takva da je jednadžba
odnosno
Ovo je parcijalna diferencijalna jednadžba koja može biti i složenija od polaznog problema. Stoga nalaženje integrirajućeg faktora općenito nije jednostavno. No, kada je integrirajući faktor funkcija samo jedne varijable (
odnosno
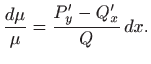
Dakle,
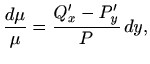
ukoliko je kvocijent na desnoj strani funkcija od
Kako je
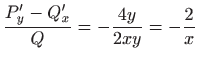
zaključujemo da je
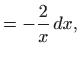 |
||
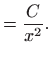 |
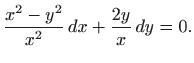
Postupak opisan na početku poglavlja daje:
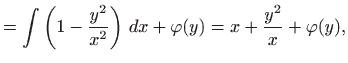 |
||
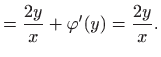 |
pa je rješenje zadane jednadžbe dano s