Prema Newtonovom drugom zakonu
gibanja
ako se tijelo kreće po pravcu i ako je gibanje tijela dano funkcijom ![]() ,
onda je sila
,
onda je sila ![]() koja djeluje na tijelo u smjeru kretanja jednaka umnošku
mase tijela i njegove akceleracije:
koja djeluje na tijelo u smjeru kretanja jednaka umnošku
mase tijela i njegove akceleracije:
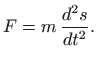
U slučaju konstantnog ubrzanja, sila
U slučaju kada sila nije konstantna, postupamo na sljedeći način:
neka se tijelo giba uzduž ![]() -osi od točke
-osi od točke ![]() do točke
do točke ![]() i neka u
točki
i neka u
točki ![]() na tijelo djeluje sila
na tijelo djeluje sila ![]() . Neka je
. Neka je
![]() podjela segmenta
podjela segmenta ![]() (vidi definiciju 2.1) takva da su svi
podintervali jednake duljine,
(vidi definiciju 2.1) takva da su svi
podintervali jednake duljine,
![]() .
U podintervalu
.
U podintervalu
![]() odaberimo točku
odaberimo točku ![]() . Kako je za veliki
. Kako je za veliki
![]() duljina intervala
duljina intervala ![]() mala, a funkcija
mala, a funkcija ![]() je neprekidna, možemo
pretpostaviti da je
je neprekidna, možemo
pretpostaviti da je ![]() gotovo konstantna na intervalu
gotovo konstantna na intervalu
![]() . Stoga je rad koji se izvrši prilikom pomicanja tijela od
točke
. Stoga je rad koji se izvrši prilikom pomicanja tijela od
točke ![]() do točke
do točke ![]() približno jednak
približno jednak
pa je cjelokupni rad približno jednak
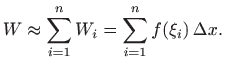
Intuitivno je jasno da ova aproksimacija postaje sve bolja što je
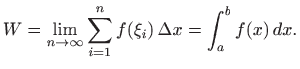
U metričkom sustavu masa se mjeri u kilogramima (kg), pomak u metrima (m)
vrijeme u sekundama (s) i sila u njutnima (newton,
![]() ).
Dakle, sila od 1 N koja djeluje na masu od 1 kg proizvodi ubrzanje od
).
Dakle, sila od 1 N koja djeluje na masu od 1 kg proizvodi ubrzanje od
![]() . Rad se mjeri u njutn-metrima ili džulima (joule,
. Rad se mjeri u njutn-metrima ili džulima (joule,
![]() ).
).
pri čemu je
Neka je, na primjer, sila od 30 N potrebna da bi se držala opruga koja je od svoje
prirodne duljine od
![]() rastegnuta na duljinu od
rastegnuta na duljinu od
![]() . Izračunajmo rad potreban da bi se opruga dalje rastegla na duljinu
od
. Izračunajmo rad potreban da bi se opruga dalje rastegla na duljinu
od
![]() . Prvo je potrebno odrediti
konstantu opruge
. Prvo je potrebno odrediti
konstantu opruge ![]() : prema zadanim podacima vrijedi
: prema zadanim podacima vrijedi
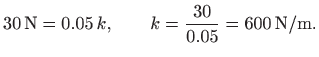
Dakle,
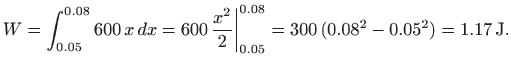
U ovom slučaju prvo treba postaviti integral. Uvedimo koordinatni sustav kao
na slici 2.25. Voda se nalazi od dubine
![]() do dubine
do dubine
![]() . Neka je
. Neka je
![]() oidjela intervala
oidjela intervala ![]() takva da su svi podintervali jednake duljine,
takva da su svi podintervali jednake duljine,
![]() .
Na taj način smo i vodu u rezervaru podijelili na
.
Na taj način smo i vodu u rezervaru podijelili na ![]() dijelova pri
čemu je
dijelova pri
čemu je ![]() -ti dio približno jednak cilindru visine
-ti dio približno jednak cilindru visine ![]() i radijusa baze
i radijusa baze
![]() . Iz sličnosti trokuta slijedi
. Iz sličnosti trokuta slijedi
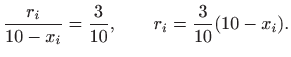
Volumen
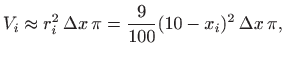
pa je masa
Sila potrebna za podizanje
Svaka čestica u
Ukupni rad potreban za ispumpavanje čitavog rezervara dobit ćemo zbrajanjem doprinosa svih
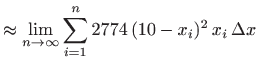 |
||
 |
||
 |
||