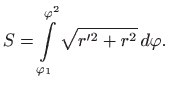×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Površina ravninskog lika     Primjene određenog integrala     Volumen rotacijskog tijela

Duljina luka ravninske krivulje

Postupak računanja duljine luka ravninske krivulje još se naziva rektifikacija krivulje. Slično kao i kod računanja površine, duljinu luka krivulje $y=f(x)$ od točke $x=a$ do točke $x=b$ računamo kao beskonačnu (integralnu) sumu beskonačno malih elemenata duljine $ds$ . Formula za element duljine slijedi iz Pitagorinog poučka i činjenice da se funkcija u okolini neke točke može aproksimirati njenom tangentom (slika 2.21),

$$ds=\sqrt{ dx^2+ dy^2}=\sqrt{1+\bigg(\frac{ dy}{ dx}\bigg)^2} dx= \sqrt{1+y^{\prime 2}} dx.$$ (2.4)

Ovdje po dogovoru uzimamo da je duljina luka pozitivna ako $x$ raste, odnosno $dx>0$ . Dakle, duljina luka krivulje $y=f(x)$ od točke $x=a$ do točke $x=b$ računa se formulom

$$S=\int\limits _{[a,b]} ds =\int\limits _a^b \sqrt{1+y^{\prime 2}} dx.$$

Slika 2.21: Element duljina luka ravninske krivulje

Primjer 2.13   Izračunajmo duljinu luka kvadratne parabole $y=x^2$ od 0 do $1$ . Na slici 2.5 vidimo da za traženu duljinu $S$ vrijedi $\sqrt{2}< S< 2$ . Koristeći, na primjer, metodu neodređenih koeficijenata iz poglavlja 1.7.3, imamo

$$S =\int\limits _0^1 \sqrt{1+4 x^2} dx= \frac{1}{2} x\sqrt{1+4 x^2} +\frac{1}{4} \ln \vert 2 x+\sqrt{1+4 x^2}\vert \bigg\vert _0^1$$

$$=\frac{\sqrt{5}}{2}+\frac{1}{4}\ln (2+\sqrt{5}) \approx 1.4789.$$

Parametarski zadana krivulja

Kod parametarski zadane krivulje,

$$x=\varphi (t),\qquad y=\psi(t), \qquad t\in \mathcal{D}\subseteq \mathbb{R},$$

element duljine luka dan je s^2.1

$$ds=\sqrt{ dx^2+ dy^2}=\sqrt{\bigg(\frac{ dx}{dt}\bigg)^2+ \bigg(\frac{ dy}{dt}\bigg)^2} dt=\sqrt{\dot x^2+\dot y^2} dt,$$

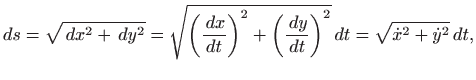
pa se duljina luka računa formulom

$$S=\int\limits _{t_1}^{t_2} \sqrt{\dot x^2+\dot y^2} dt.$$

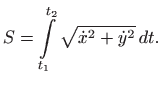
Iz ove formule slijedi da je duljina luka pozitivna kada je $dt$ nenegativan, odnosno kada $t$ raste.

Primjer 2.14  

a)

Opseg kružnice radijusa $r$ ,

$$x=r\cos t,\qquad y=r\sin t,\qquad t\in[0,2\pi],$$

jednak je

$$S=\int\limits _0^{2\pi} \sqrt{(r(-\sin t))^2+(r\cos t)^2} dt= \int\limits _0^{2\pi} r dt= r t \bigg\vert _0^{2\pi}=2 r \pi.$$

b)

Duljina jednog luka cikloide iz primjera 2.9 (slika 2.16) jednaka je

$$S=\int\limits _0^{2\pi} \sqrt{[a (1-\cos t)]^2+ (a\sin t)^2} dt= a\int\limits _0^{2\pi}\sqrt{2-2\cos t} dt.$$

Koristeći poznatu vezu između trigonometrijskih funkcija,

$$\sin^2\frac{t}{2}=\frac{1}{2}(1-\cos t),$$

i činjenicu da je $\sin\frac{t}{2}\geq 0$ za $t\in[0,2\pi]$ , imamo

$$S=2 a \int\limits _0^{2\pi} \sin \frac{t}{2} dt= -4 a\cos \frac{t}{2} \bigg\vert _0^{2\pi} =8 a.$$

Krivulja zadana u polarnim koordinatama

Krivulja zadana u polarnim koordinatama,

$$r=r(\varphi ),\qquad \varphi \in[\varphi _1,\varphi _2],$$

prvo se pomoću transformacija (2.3) prebaci u parametarski oblik,

$$x =r\cos \varphi =r(\varphi )\cos\varphi ,$$

$$y =r\sin \varphi = r(\varphi )\sin\varphi .$$ (2.5)

Sada je

$$\dot x=r'(\varphi )\cos \varphi +r(\varphi ) (-\sin\varphi ), \qquad \dot y=r'(\varphi )\sin \varphi +r(\varphi ) \cos\varphi ,$$

odnosno

$$\dot x^2+\dot y^2 = \quad (r'(\varphi ))^2\cos^2\varphi + r^2(\varphi )\sin^2\varphi - 2r'(\varphi )r(\varphi )\sin\varphi \cos \varphi$$

$$\quad +(r'(\varphi ))^2\sin^2\varphi + r^2(\varphi )\cos^2\varphi + 2r'(\varphi )r(\varphi )\sin\varphi \cos \varphi$$

$$=\quad (r'(\varphi ))^2+r^2(\varphi ).$$

Dakle, duljina luka krivulje u polarnim koordinatama računa se formulom^2.2

$$S= \int\limits _{\varphi _1}^{\varphi ^2} \sqrt{r^{\prime 2} +r^2} d\varphi .$$

Primjer 2.15   Duljina luka prvog zavoja Arhimedove spirale (vidi primjer 2.12 i sliku 2.20) jednaka je

$$S =\int\limits _0^{2\pi}\sqrt{a^2+(a \varphi )^2} d\varphi = a\int\limits _0^{2\pi} \sqrt{1+\varphi ^2} d\varphi =\cdots$$

$$= a\bigg(\frac{1}{2}\varphi \sqrt{1+\varphi ^2} + \frac{1}{2}\ln ... ...hi +\sqrt{1+\varphi ^2}\vert \bigg) \bigg\vert _0^{2\pi} \approx 21.256 a.$$

Površina ravninskog lika     Primjene određenog integrala     Volumen rotacijskog tijela