×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 METODA NAJMANJIH KVADRATA I     METODA NAJMANJIH KVADRATA I     QR rastav vektora i

Linearna regresija

U tablici su navedeni podaci o broju utrošenih minuta na pozive u nepokretnoj i pokretnim telefonskim mrežama (u milijunima) kroz godine:

godina	$2006$	$2007$	$2008$	$2009$	$2010$
nepokretna m.	$8 515$	$5 392$	$5 557$	$5 276$	$5 099$
pokretne m.	$4 115$	$4 985$	$5 657$	$5 981$	$5 937$

Uz pretpostavku da se radi o linearnoj ovisnosti, izračunajte regresijske pravce i predvidite odnos broja utrošenih minuta u nepokretnoj i pokretnim telefonskim mrežama na pozive u 2012. godini.

Rješenje.

Pronađimo najprije regresijski pravac $y=kx+l$ za točke $T_1=(2006,8515)$ , $T_2=(2007,5392)$ , $T_3=(2008,5557)$ , $T_4=(2009,5276)$ i $T_5=(2010,5099)$ .

Očito ne postoji pravac koji prolazi kroz sve zadane točke. Prema [M2, poglavlje 6.1.1], pravac $y=kx+l$ će "najbolje" prolaziti kroz zadane točke ako su $k$ i $l$ rješenja preodređenog sustava

$2006k$	$+$	$l$	$=$	$8 515$
$2007k$	$+$	$l$	$=$	$5 392$
$2008k$	$+$	$l$	$=$	$5 557$
$2009k$	$+$	$l$	$=$	$5 276$
$2010k$	$+$	$l$	$=$	$5 099$ .

u smislu najmanjih kvadrata. U matričnom obliku sustav glasi

$$A \mathbf{y}=\mathbf{b},$$

gdje je

$$A= \begin{bmatrix} 2006 & 1 2007 & 1 2007 & 1 20... ...matrix} 8 515 5 392 5 557 5 276 5 099 \end{bmatrix}.$$

Rješenje sustava u smislu najmanjih kvadrata je rješenje normalne jednadžbe

$$A^T A \mathbf{x}=A^T \mathbf{b}$$.

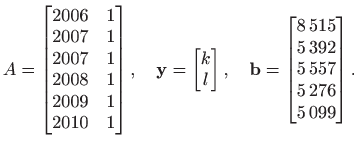Uvrštavanjem dobivamo sustav od dvije jednadžbe s dvije nepoznanice

$$\begin{bmatrix} 20 160 330 & 10 040 10 040 & 5 \end{bm... ...l \end{bmatrix} = \begin{bmatrix} 59 909 764 29 839 \end{bmatrix}.$$

Ovaj sustav ima jedinstveno rješenje

$$\begin{bmatrix} k l \end{bmatrix} =(A^T A)^{-1}A^T \mathb... ...39 \end{bmatrix} = \begin{bmatrix} -694.8 1 401 126.2 \end{bmatrix}$$

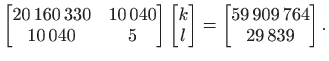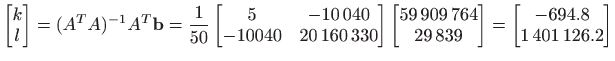Jednadžba regresijskog pravca je

$$y=-694.8x+1 401 126.2,$$

a broj utrošenih minuta na pozive u nepokretnoj mreži (koji se s vremenom smanjuje) u 2012. godini bi trebao biti približno

$$y(2012)=-694.8\cdot 2012+1 401 126.2=3 188.6$$.

Na isti način pronaći ćemo i regresijski pravac za točke $S_{1}=(2006,4 115)$ , $S_{2}=(2007,4 985)$ , $S_{3}=(2008,5 657)$ , $S_{4}=(2009,5 981)$ i $S_{5}=(2010,5937))$ .

Kao i u prvom slučaju, pravac $y=kx+l$ će najbolje prolaziti kroz zadane točke u smislu najmanjih kvadrata ako su $k$ i $l$ rješenja preodređenog sustava

$2006k$	$+$	$l$	$=$	$4 115$
$2007k$	$+$	$l$	$=$	$4 985$
$2008k$	$+$	$l$	$=$	$5 657$
$2009k$	$+$	$l$	$=$	$5 981$
$2010k$	$+$	$l$	$=$	$5 937$ ,

ili, u matričnom obliku,

$$A \mathbf{y}=\mathbf{b},$$

gdje je

$$A= \begin{bmatrix} 2006 & 1 2007 & 1 2008 & 1 20... ...$4 985$ $5 657$ $5 981$ $5 937$ \end{tabular} \right] .$$

Normalna jednadžba glasi

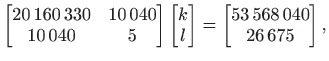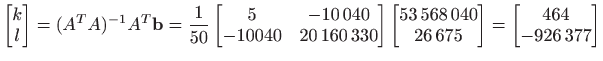$$\begin{bmatrix} 20 160 330 & 10 040 10 040 & 5 \end{bm... ...l \end{bmatrix} = \begin{bmatrix} 53 568 040 26 675 \end{bmatrix},$$

a njeno rješenje je

$$\begin{bmatrix} k l \end{bmatrix} =(A^{T}A)^{-1}A^{T}\mat... ... 26 675 \end{bmatrix} = \begin{bmatrix} 464 -926 377 \end{bmatrix}$$

Prema tome, jednadžba regresijskog pravca je

$$y=464x-926 377,$$

a broj utrošenih minuta na pozive u pokretnoj mreži (koji se s vremenom povećava) u 2012. godini bi trebao biti otprilike

$$y(2012)=464\cdot 2012-926 377=7 191$$

METODA NAJMANJIH KVADRATA I     METODA NAJMANJIH KVADRATA I     QR rastav vektora i