Dvostruki integral računamo uzastopnim računanjem dva jednostruka integrala pomoću Newton-Leibnitzove formule (vidi poglavlje 2.2). Opisat ćemo postupak integriranja u slučajevima kada je područje integracije:
Dokaz teorema temelji se na svojstvu da kod dvostrukih suma možemo zamijeniti poredak zbrajanja, odnosno
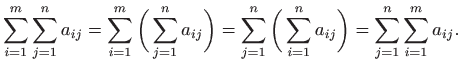
Detalje dokaza izostavljamo.
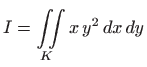
pri čemu je
![$\displaystyle = \int\limits _a^b \bigg(\int\limits _c^d x y^2 dy\bigg) d...
...gg] dx = \int\limits _a^b x \bigg( \frac{d^3}{3}-\frac{c^3}{3}\bigg) dx$](img2062.gif) |
||
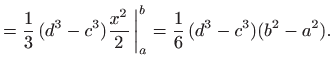 |
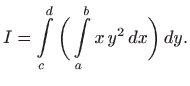
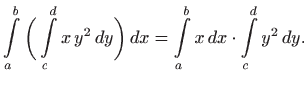
Ako je područje integracije ![]() zadano dvama neprekidnim funkcijama,
zadano dvama neprekidnim funkcijama,
onda je
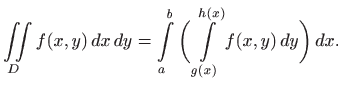
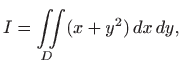
pri čemu je
Vidimo da je
pa je
![$\displaystyle = \int\limits _{-1}^1 \bigg( \int\limits _{x^4}^{x^2} (x+y^2) d...
... dx= \int\limits _{-1}^1 \bigg[ xy +\frac{y^3}{3} \bigg]_{x^4}^{x^2} dx$](img2072.gif) |
||
![$\displaystyle =\int\limits _{-1}^1 \bigg( x^3 +\frac{x^6}{3} -x^5 -\frac{x^{12}...
...rac{x^7}{21}-\frac{x^6}{6} -\frac{x^{13}}{39} \bigg]_{-1}^{1} = \frac{4}{91}.$](img2073.gif) |
![$\displaystyle I=\int\limits _{0}^1 \bigg( \int\limits _{-\sqrt[4]{y}}^{-\sqrt{y...
...limits _{\sqrt{y}}^{\sqrt[4]{y}} (x+y^2) dx\bigg) dy
=\cdots=\frac{4}{91}.
$](img2080.gif)
Približna vrijednost dvostrukog integrala može se dobiti koristeći Java program koji računa odgovarajuću integralnu sumu prema definiciji 4.1.