Težište ravne ploče
![]() zadanog oblika je točka
zadanog oblika je točka
![]() sa svojstvom da se ploča poduprta u toj točki nalazi u položaju ravnoteže
(slika 2.28).
sa svojstvom da se ploča poduprta u toj točki nalazi u položaju ravnoteže
(slika 2.28).
Izvod formule za težište započet ćemo poznatim Arhimedovim
zakonom poluge: poluga kojoj se na kraju ![]() nalazi masa
nalazi masa ![]() ,
a na kraju
,
a na kraju ![]() nalazi masa
nalazi masa ![]() te koja je poduprta u točki
te koja je poduprta u točki ![]() , bit
će u ravnoteži
ako je (slika 2.29)
, bit
će u ravnoteži
ako je (slika 2.29)
iz čega slijedi
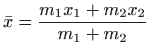
Broj ![]() je moment mase
je moment mase ![]() u odnosu na
ishodište. Slično, težište sustava od
u odnosu na
ishodište. Slično, težište sustava od ![]() čestica s masama
čestica s masama
![]() ,
koje se nalaze u točkama
,
koje se nalaze u točkama
![]() na
na ![]() -osi, nalazi se u točki
-osi, nalazi se u točki
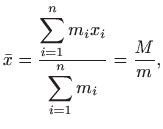
pri čemu je
Poopćimo sada razmatranje na sustav od ![]() čestica s masama
čestica s masama
![]() ,
koje se nalaze u točkama s koordinatama
,
koje se nalaze u točkama s koordinatama
![]() u
u ![]() -ravnini. Moment sustava oko
-ravnini. Moment sustava oko ![]() -osi jednak je
-osi jednak je
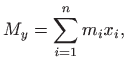
moment sustava oko
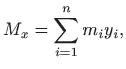
a težište sustava je u točki
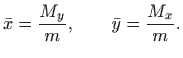
Promotrimo sada ravnu ploču
![]() uniformne gustoće
uniformne gustoće ![]() omeđenu s
omeđenu s
![]() -osi, pravcima
-osi, pravcima ![]() i
i ![]() i neprekidnim funkcijama
i neprekidnim funkcijama ![]() i
i ![]() , pri čemu je
, pri čemu je
![]() za
za ![]() (vidi sliku 2.30).
(vidi sliku 2.30).
Neka je
![]() podjela intervala
podjela intervala ![]() takva da su svi
podintervali jednake duljine,
takva da su svi
podintervali jednake duljine,
![]() . U
. U
![]() -tom intervalu odaberimo središnju točku
-tom intervalu odaberimo središnju točku
![]() .
Za dovoljno mali
.
Za dovoljno mali ![]() dio ploče
dio ploče
![]() od točke
od točke ![]() do
točke
do
točke ![]() možemo aproksimirati pravokutnikom
možemo aproksimirati pravokutnikom ![]() kao na slici
2.30. Zbog uniformne gustoće ploče, težište pravokutnika
kao na slici
2.30. Zbog uniformne gustoće ploče, težište pravokutnika ![]() se
nalazi u točki
se
nalazi u točki
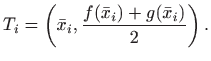
Masa pravokutnika
Moment pravokutnika
Zbrajanjem ovih momenta i uzimanje limesa kada
![$\displaystyle M_y=\lim_{n\to\infty} \sum_{i=1}^n \rho \bar x_i [f(\bar x_i)-g(\bar
x_i)] \Delta x
= \rho \int_a^b x [f(x)-g(x)] dx.
$](img1091.gif)
Slično, moment pravokutnika
![$\displaystyle M_x(P_i)=\rho [f(\bar x_i)-g(\bar x_i)] \Delta x
\frac{f(\bar x_i)+g(\bar x_i)}{2}
$](img1092.gif)
pa je ukupni moment ploče
![$\displaystyle M_x=\lim_{n\to\infty} \sum_{i=1}^n \rho \frac{1}{2} [f(\bar ...
...2-g(\bar
x_i)^2] \Delta x
= \rho \int_a^b \frac{1}{2} [f(x)^2-g(x)^2] dx.
$](img1093.gif)
Ukupna masa ploče jednaka je umnošku gustoće i površine,
![$\displaystyle m=\rho \int_a^b [f(x)-g(x)] dx.
$](img1094.gif)
Težište ploče nalazi se u točki
![$\displaystyle =\frac{\rho\displaystyle \int_a^b x [f(x)-g(x)] dx}{\rho \disp...
...aystyle \int_a^b x [f(x)-g(x)] dx}{\displaystyle \int_a^b [f(x)-g(x)] dx},$](img1098.gif) |
||
![$\displaystyle =\frac{\rho\displaystyle \int_a^b \frac{1}{2} [f(x)^2-g(x)^2] ...
...^b \frac{1}{2} [f(x)^2-g(x)^2] dx}{\displaystyle \int_a^b [f(x)-g(x)] dx}.$](img1100.gif) |