☰
matematika2
DIFERENCIJALNE JEDNADŽBE
DIFERENCIJALNE JEDNADŽBE
Populacijska jednadžba
Uvod
- a)
- Provjerite je li
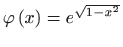 rješenje diferencijalne jednadžbe
rješenje diferencijalne jednadžbe
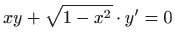 .
.
- b)
- Pokažite da je svaki član familije krivulja
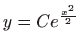 rješenje diferencijalne jednadžbe
rješenje diferencijalne jednadžbe
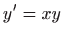 , te odredite ono rješenje koje zadovoljava
početni uvjet
, te odredite ono rješenje koje zadovoljava
početni uvjet
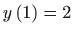 .
.
- c)
- Odredite diferencijalnu jednadžbu čije je rješenje
familija krivulja
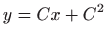 .
.
- d)
- Odredite krivulju iz familije krivulja
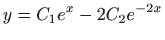 za koju je
za koju je
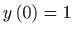 i
i
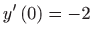 .
.
Rješenje.
- a)
- Provjeru vršimo uvrštavanjem
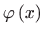 u
zadanu diferencijalnu jednadžbu. Prvo računamo derivaciju od
u
zadanu diferencijalnu jednadžbu. Prvo računamo derivaciju od
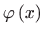
Uvrštavanjem dobivamo
Dakle,
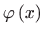 jest rješenje diferencijalne
jednadžbe
jest rješenje diferencijalne
jednadžbe
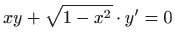 .
.
- b)
- Uvrštavanjem
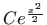 u zadanu diferencijalnu
jednadžbu
u zadanu diferencijalnu
jednadžbu
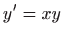 , dobivamo
, dobivamo
pa
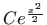 jest rješenje diferencijalne jednadžbe
jest rješenje diferencijalne jednadžbe
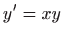 . Preostaje još pronaći ono
rješenje koje zadovoljava početni uvjet
. Preostaje još pronaći ono
rješenje koje zadovoljava početni uvjet
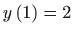 .
.
Traženo partikularno rješenje dobije se uvrštavanjem dobivene
konstante 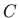 u opće rješenje.
u opće rješenje.
- c)
- Zadanu familiju krivulja prvo deriviramo s ciljem eliminiranja
konstante
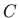 :
:
Uvrštavanjem u zadanu diferencijalnu jednadžbu dobivamo
- d)
- Vrijedi
Uvrštavanjem početnih uvjeta dobivamo
Rješenje sustava
je
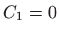 i
i
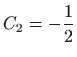 , pa se tra
žena krivulja dobije uvrštavanjem tih konstanti u zadanu familiju
krivulja:
, pa se tra
žena krivulja dobije uvrštavanjem tih konstanti u zadanu familiju
krivulja:
DIFERENCIJALNE JEDNADŽBE
DIFERENCIJALNE JEDNADŽBE
Populacijska jednadžba
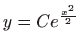 rješenje diferencijalne jednadžbe
rješenje diferencijalne jednadžbe
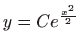 rješenje diferencijalne jednadžbe
rješenje diferencijalne jednadžbe
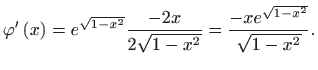
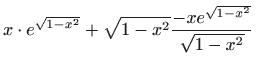
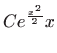
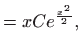
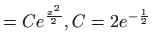
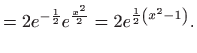
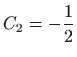 , pa se tra
žena krivulja dobije uvrštavanjem tih konstanti u zadanu familiju
krivulja:
, pa se tra
žena krivulja dobije uvrštavanjem tih konstanti u zadanu familiju
krivulja: