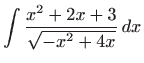 .
.
Izračunajte integral
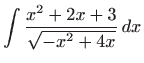 .
.
Rješenje.
Iz formule za metodu neodređenih koeficijenata
![]() [M2, poglavlje 1.7.3], slijedi
[M2, poglavlje 1.7.3], slijedi
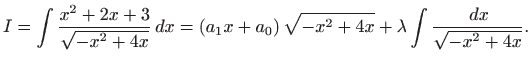
Deriviranjem po
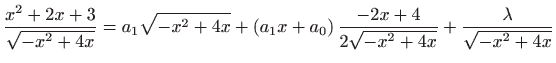
Pomnožimo li cijeli izraz sa
Izjednačavanjem lijeve i desne strane dobivamo
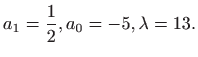
Integral ![]() sada je jednak
sada je jednak
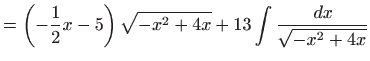 |
||
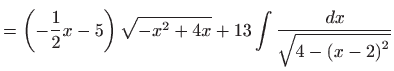 |
||
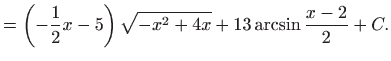 |