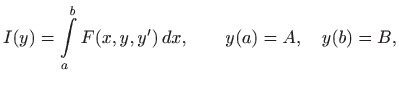
U ovom poglavlju opisat ćemo Eulerovu metodu konačnih razlika za numeričko rješavanje problema. Metoda se temelji na ideji da kod traženja ekstrema funkcionala
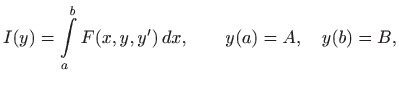
ne promatramo sve dozvoljene derivabilne funkcije koje zadovoljavaju rubne uvjete, već samo poligonalne linije koje imaju vrhove u točkama
koje su definirane na sljedeći način: uz
Na ovaj način zadani funkcional
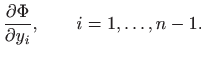
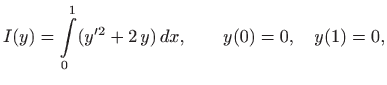
metodom konačnih razlika. Odaberimo
pri čemu se derivacije aproksimiraju konačnim razlikama
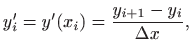
odnosno
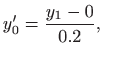 |
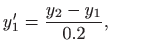 |
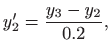 |
||
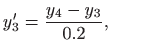 |
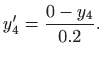 |
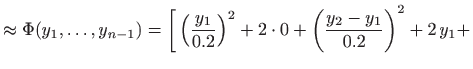 |
||
![$\displaystyle \quad + \left(\frac{y_3-y_2}{0.2}\right)^2 + 2 y_2 + \left(\fra...
...\right)^2 + 2 y_3 + \left(\frac{-y_4}{0.2}\right)^2 + 2 y_4 \bigg]\cdot 0.2.$](img2626.gif) |
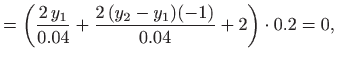 |
||
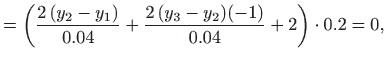 |
||
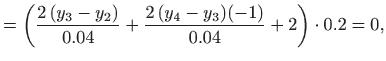 |
||
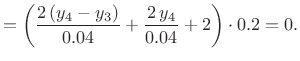 |
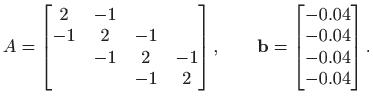
Rješenje sustava je
Primijetimo da se izračunane vrijednosti poklapaju s vrijednostima rješenja
Rješenje se može jednostavno programirati u programskom jeziku
Matlab. Program koji postavi matricu ![]() i vektor
i vektor
![]() te potom riješi sustav i nacrta numeričko i egzaktno rješenje glasi:
te potom riješi sustav i nacrta numeričko i egzaktno rješenje glasi:
Octave On-line[Octave On-line Home] [Octave User's Guide] |