U prethodnom poglavlju izveli smo dvije zamjene varijabla: iz Kartezijevih u
cilindrične i iz Kartezijevih u sferne koordinate. No, problem zamjene
varijabli u višestrukom
integralu
je općeniti problem koji ima općenito
rješenje. Za trostruki integral (![]() ) postupak je dan sljedećim teoremom kojeg navodimo
bez dokaza.
) postupak je dan sljedećim teoremom kojeg navodimo
bez dokaza.
U prethodnom teoremu varijable ![]() ,
, ![]() i
i ![]() mogu biti varijable u bilo
kojem koordinatnom sustavu (ne nužno Kartezijevom). Zamjena varijabli se na
analogan način definira i za ostale dimenzije (
mogu biti varijable u bilo
kojem koordinatnom sustavu (ne nužno Kartezijevom). Zamjena varijabli se na
analogan način definira i za ostale dimenzije (![]() ,
, ![]() ,
, ![]() , ...).
, ...).
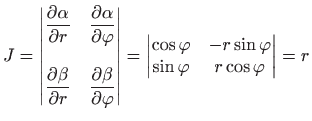
pa, zbog