☰
matematika2
Cilindrične koordinate u trostrukom
VIŠESTRUKI INTEGRALI
Volumen tijela
Sferne koordinate u trostrukom integralu
Izračunajte integral
ako je
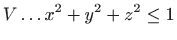 .
.
Rješenje.
Područje integracije 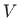 integrala prikazano je na Slici 4.13.
integrala prikazano je na Slici 4.13.
Slika:
Područje integracije
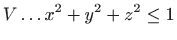 .
.
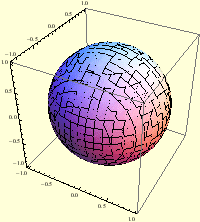 |
Prijeđimo na sferne koordinate
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 4.3.1]:
[M2, poglavlje 4.3.1]:
Jakobijan je
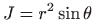 . Integriramo po cijeloj kugli, pa za nove varijable vrijedi
. Integriramo po cijeloj kugli, pa za nove varijable vrijedi
i imamo
Cilindrične koordinate u trostrukom
VIŠESTRUKI INTEGRALI
Volumen tijela
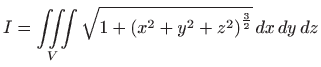
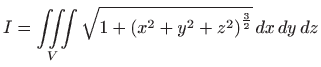
![]() integrala prikazano je na Slici 4.13.
integrala prikazano je na Slici 4.13.
![]() [M2, poglavlje 4.3.1]:
[M2, poglavlje 4.3.1]:
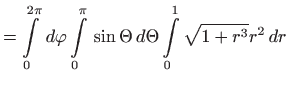
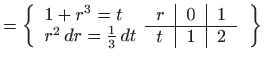
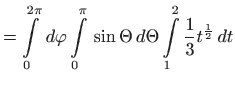
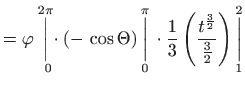
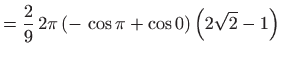
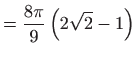 .
.