☰
matematika2
FUNKCIJE VIŠE VARIJABLA
FUNKCIJE VIŠE VARIJABLA
Parcijalna derivacija prvog reda
Područje definicije funkcije
Odredite područje definicije funkcija:
- a)
-
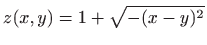 ,
,
- b)
-
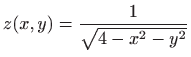 ,
,
- c)
-
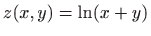 ,
,
- d)
-
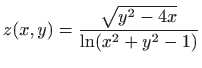 ,
,
- e)
-
 .
.
Rješenje.
- a)
- Da bi zadana funkcija bila dobro definirana mora vrijediti
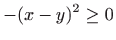 , , |
|
to jest
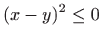 . . |
|
To je ispunjeno samo kada je
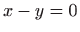 , odnosno
, odnosno
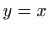 , pa je područje definicije zadane funkcije
dano sa
, pa je područje definicije zadane funkcije
dano sa
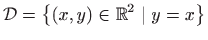 (slika 3.1).
(slika 3.1).
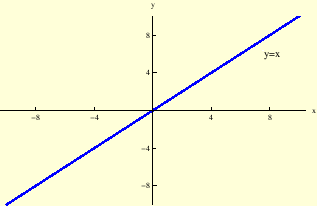
Slika:
Područje definicije funkcije
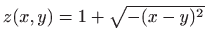
 |
- b)
- Zadana funkcija definirana je na području
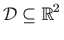 koje je određeno
nejednadžbom
koje je određeno
nejednadžbom
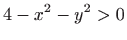 , odnosno (slika 3.2)
, odnosno (slika 3.2)
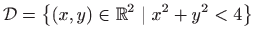 . . |
|
Slika:
Područje definicije funkcije
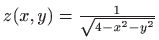
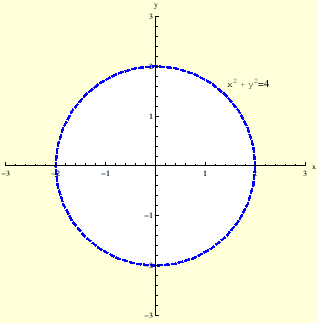 |
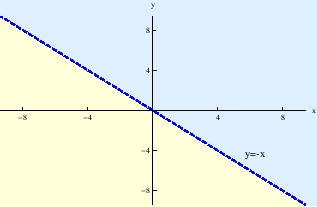
- c)
- Funkcija
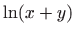 definirana je za sve točke
definirana je za sve točke
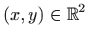 za koje je
za koje je
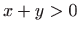 ,
odnosno na području (slika 3.3)
,
odnosno na području (slika 3.3)
Slika:
Područje definicije funkcije
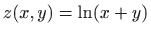
 |
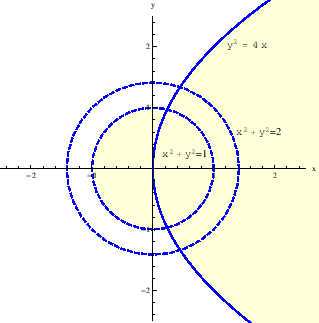
- d)
- Zadana funkcija će biti dobro definirana ako ispunjeni sljedeći uvjeti:
Dakle, područje definicije zadane funkcije je (vidi sliku 3.4):
Slika:
Područje definicije funkcije
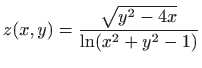
 |
- e)
- Prema definiciji funkcije
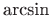
![[*]](../icons.gif/crossref.gif) [M1, poglavlje 4.6.6], zaključujemo da domena zadane funkcije mora ispunjavati sljedeće uvjete:
[M1, poglavlje 4.6.6], zaključujemo da domena zadane funkcije mora ispunjavati sljedeće uvjete:
Drugi uvjet je ispunjen ako su 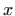 i
i 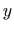 istog predznaka.
Dakle (vidi sliku 3.5),
istog predznaka.
Dakle (vidi sliku 3.5),
Slika:
Područje definicije funkcije

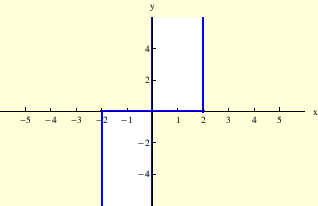 |
FUNKCIJE VIŠE VARIJABLA
FUNKCIJE VIŠE VARIJABLA
Parcijalna derivacija prvog reda
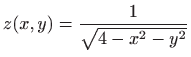 ,
,
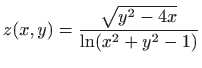 ,
,
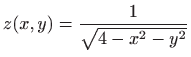 ,
,
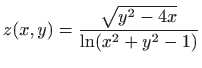 ,
,