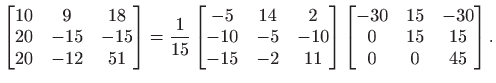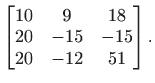 |
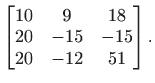 |
Rješenje.
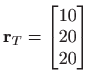 točke
točke
Budući se točka
![]() nalazi na negativnom dijelu osi apscisa,
ordinata i aplikata su joj 0
. Od ishodišta je jednako udaljena kao i točka
nalazi na negativnom dijelu osi apscisa,
ordinata i aplikata su joj 0
. Od ishodišta je jednako udaljena kao i točka ![]() , pa
joj je apscisa
, pa
joj je apscisa ![]() , odnosno
, odnosno
![]() .
.
Sada vektor
![]() moramo rotirati u
moramo rotirati u
![]() , što znači da moramo pronaći matricu
, što znači da moramo pronaći matricu ![]() za koju je
za koju je
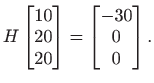 |
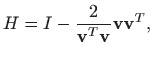 gdje je
gdje je
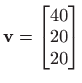 i
i 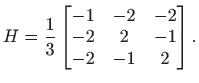
Lako se provjeri da je
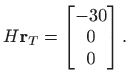
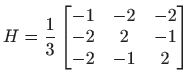
koji prvi stupac matrice
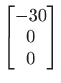 .
.
Kod QR rastava vektora, matrica ![]() je upravo Householderov reflektor,
pa QR rastav prvog stupca matrice
je upravo Householderov reflektor,
pa QR rastav prvog stupca matrice ![]() glasi
glasi
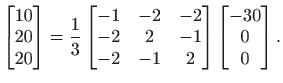
Označimo
![$\displaystyle Q_1 A = \left[ \begin{array}{c\vert c}
-30 & \begin{array}{cc} \...
...t]=\begin{bmatrix}-30& 15& -30 0 & -12 & -39 0 & -9 & 27 \end{bmatrix}.
$](img2482.gif)
Sada pronađimo Householderov reflektor ![]() koji je pridružen prvom stupcu
koji je pridružen prvom stupcu
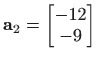 matrice
matrice
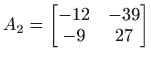 .
.
Norma vektora
![]() je
je
![]() , što
znači da vektor
, što
znači da vektor
![]() treba zarotirati u
treba zarotirati u
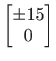 .
Predznak se u praksi (zbog numeričke stabilnosti) bira tako da se izbjegne oduzimanje.
U našem slučaju to je ``
.
Predznak se u praksi (zbog numeričke stabilnosti) bira tako da se izbjegne oduzimanje.
U našem slučaju to je ``![]() ''.
Dakle,
''.
Dakle,
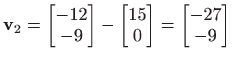 i
i 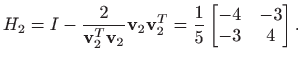
Stavimo
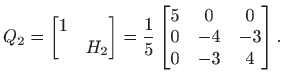
Sada je
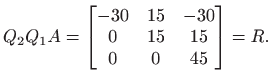
Matrice
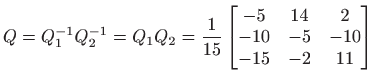
pa QR rastav matrice