×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 QR rastav vektora i     QR rastav     Numeričko računanje QR rastava

QR rastav matrice

QR rastav matrice nalazimo rekurzivnom primjenom QR rastava vektora. Postupak ćemo ilustrirati na matrici tipa $5\times 3$ . Neka je $\mathbf{a}_1$ prvi stupac matrice $A$ i neka je

$$H_1 \mathbf{a}_1 = \begin{bmatrix}\pm \Vert\mathbf{a}_1\Vert 0 0 0 0 \end{bmatrix}$$

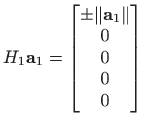
rastav vektora $\mathbf{a}_1$ izračunan prema postupku opisanom u prethodnom poglavlju. Stavimo $Q_1=H_1$ . Tada je

$$Q_1 A = \left[ \begin{array}{c\vert c} \pm \Vert\mathbf{a}_1\Vert... ...\\ \hline \begin{array}{c}0 0 0 0\end{array} & A_2 \end{array}\right].$$

Neka je $\mathbf{a}_2$ prvi stupac matrice $A_2$ koja je tipa $4\times 2$ i neka je

$$H_2 \mathbf{a}_2 = \begin{bmatrix}\pm \Vert\mathbf{a}_2\Vert 0 0 0 \end{bmatrix}$$

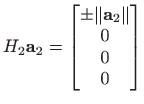
QR rastav vektora $\mathbf{a}_2$ . Stavimo

$$Q_2=\begin{bmatrix}1 & & H_2 \end{bmatrix}.$$

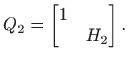
Tada je

$$Q_2 Q_1 A = \left[ \begin{array}{cc\vert c} \begin{array}{c}... ...gin{array}{c}0 0 0 \end{array}& A_3 \end{array} \right]$$

pri čemu je matrica $A_3$ tipa $3\times 1$ . Konačno, neka je $\mathbf{a}_3=A_3$ i neka je

$$H_3 \mathbf{a}_3 = \begin{bmatrix}\pm \Vert\mathbf{a}_3\Vert 0 0 \end{bmatrix}$$

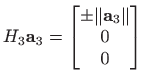
QR rastav vektora $\mathbf{a}_3$ . Stavimo

$$Q_3=\begin{bmatrix}1 & & & 1 & & & H_3 \end{bmatrix}.$$

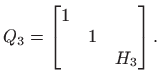
Tada je

$$Q_3 Q_2 Q_1 A = \begin{bmatrix}\pm \Vert\mathbf{a}_1\Vert &\times... ...0 & 0 & \pm \Vert\mathbf{a}_3\Vert \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{bmatrix}=R.$$

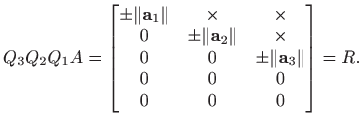
Zbog ortogonalnosti i simetričnosti matrica $Q_i$ , $i=1,2,3$ , za matricu $Q=Q_1 Q_2 Q_3$ vrijedi

$$Q Q_3Q_2Q_1A= A=QR$$

pa smo tako dobili QR rastav matrice $A$ . Ovaj postupak je lako poopćiti na matricu bilo koje dimenzije.