Za prikaz po komponentama vrijedi
što se vidi uvrštavanjem prikaza 1.1 u gornji limes. Drugim riječima, funkcija
Slično kao u
![]() [M1, poglavlje 5.1], derivaciju također možemo definirati
pomoću izraza
[M1, poglavlje 5.1], derivaciju također možemo definirati
pomoću izraza
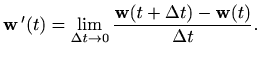
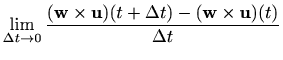 |
|||
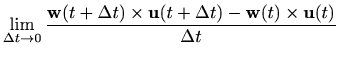 |
|||
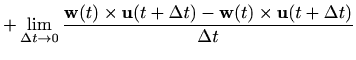 |
|||
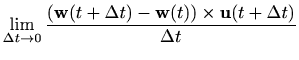 |
|||
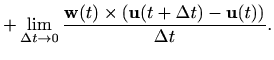 |
Diferencijal definiramo slično kao kod funkcije jedne varijable
![]() [M1,
poglavlje 5.2]:
[M1,
poglavlje 5.2]:
Teorem 1.1 vrijedi i za diferencijale.
Formulu za derivaciju složene funkcije daje nam sljedeći teorem kojeg navodimo bez dokaza.