Neka ![]() označava skup svih radijus-vektora u pravokutnom koordinatnom sustavu
označava skup svih radijus-vektora u pravokutnom koordinatnom sustavu
![]()
![]() [M1, poglavlje 3.4],
[M1, poglavlje 3.4],
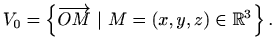
Za svaku točku ![]() je
je
![]() radijus-vektor pa ga možemo razložiti po
komponentama:
radijus-vektor pa ga možemo razložiti po
komponentama:
Za razliku od funkcija jedne ili više varijabli koje smo razmatrali u
kolegijima Matematika 1 i Matematika 2, vektorske funkcije nemaju graf u
klasičnom smislu te riječi. Umjesto toga definiramo hodograf ili trag vektorske funkcije
![]() kao skup svih točaka koje opisuju vrhovi
radijus-vektora
kao skup svih točaka koje opisuju vrhovi
radijus-vektora
![]() kada
kada ![]() poprima vrijednosti iz domene
poprima vrijednosti iz domene ![]() .
.
zadana je cilindrična eliptička spirala. Krivulja leži na plaštu eliptičkog cilindra [M2, poglavlje 3.4.5]
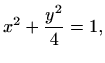
sastoji se od točaka
Od sada nadalje pretpostavit ćemo da je ![]() , odnosno
, odnosno
![]() .
.
Ova definicija je formalno jednaka definiciji limesa funkcije jedne varijable
![]() [M1, definicija 4.5], s time što
[M1, definicija 4.5], s time što
![]() označava duljinu vektora
označava duljinu vektora
![]() odnosno udaljenost vektora
odnosno udaljenost vektora
![]() i
i
![]() : ako je
: ako je
![]() zadan s (1.1) i
zadan s (1.1) i
onda je
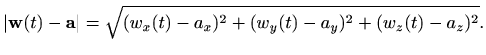
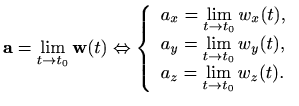
Iz ovog rastava po komponentama i definicija skalarnog i vektorskog produkta (vidi
Nakon što smo definirali limes, prirodno slijedi definicija neprekidnosti koja
je identična onoj iz
![]() [M1, poglavlje 4.4].
[M1, poglavlje 4.4].
Iz definicije neprekidnosti slijedi da je vektorska funkcija neprekidna ako i
samo ako su njene komponente ![]() ,
, ![]() i
i ![]() neprekidne funkcije.
Na primjer, funkcija
neprekidne funkcije.
Na primjer, funkcija
![]() iz primjera 1.1 ii) je očito
neprekidna.
iz primjera 1.1 ii) je očito
neprekidna.