U ovom poglavlju je
![]() , dok sa
, dok sa ![]() označavmo skup svih
radijus-vektora u sustavu
označavmo skup svih
radijus-vektora u sustavu
![]() .
.
Ako točka ![]() ima u koordinatnom sustavu
ima u koordinatnom sustavu
![]() zapis
zapis ![]() , onda je skalarno polje zadano funkcijom tri varijable
, onda je skalarno polje zadano funkcijom tri varijable
pri čemu je
pri čemu se vektor
Ako promijenimo koordinatni sustav, onda se polje naravno ne mijenja, ali se
mijenja funkcija ![]() (funkcije
(funkcije ![]() ,
, ![]() i
i ![]() ) s kojima je polje
opisano. Osnovna svojstva polja (neprekidnost i diferencijabilnost) ne ovise o
izboru koordinatnog sustava.
) s kojima je polje
opisano. Osnovna svojstva polja (neprekidnost i diferencijabilnost) ne ovise o
izboru koordinatnog sustava.
Radi jednostavnosti često ne pravimo razliku između polja ![]() i
funkcije
i
funkcije ![]() . Također, često sve prostore radijus-vektora
. Također, često sve prostore radijus-vektora ![]() identificiramo
s
identificiramo
s ![]() , odnosno sve radijus-vektore
, odnosno sve radijus-vektore
![]() nanosimo iz ishodišta.
nanosimo iz ishodišta.
zadano je skalarno polje
koje je neprekidno i diferencijabilno na području definicije.
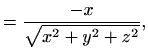 |
||
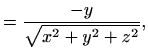 |
||
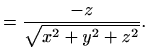 |
Na primjer, nivo-plohe u primjeru 1.4 d) su mjesta u zemljinoj atmosferi koja imaju istu gravitaciju, dok su silnice pravci koji prolaze središtem zemlje.
Na primjer, nestacionarna polja dobit ćemo ako u primjeru 1.4 a) i c) promatramo temperaturu odnosno strujanje zraka kroz neki vremenski interval.