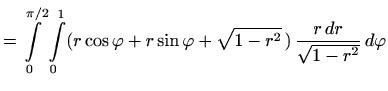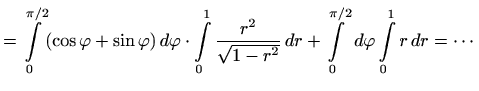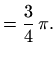☰
matematika3
Glatka ploha
PLOŠNI INTEGRALI
Plošni integral vektorskog polja
Plošni integral skalarnog polja
Definicija 3.3 Neka je
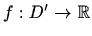
skalarno polje, gdje je
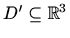
otvoren
skup. Neka je
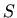
ploha sadržana u
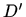
zadana funkcijom
gdje je
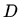
zatvoren skup omeđen s po djelovima glatkom krivuljom.
Plošni integral skalarnog polja 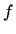 po plohi
po plohi 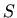
je broj
Plošni integral skalarnog polja još zovemo i integral po projekciji i
plošni integral prve vrste.
Plošni integral skalarnog polja
po po djelovima glatkoj plohi 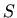 sastavljenoj od ploha
sastavljenoj od ploha
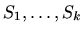 definiramo kao
definiramo kao
Ako je 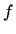 površinska gustoća plohe
površinska gustoća plohe 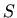 , onda
, onda
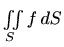 daje masu
plohe. Ako stavimo
daje masu
plohe. Ako stavimo 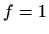 , onda
, onda
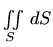 daje površinu plohe kao što smo
već vidjeli.
daje površinu plohe kao što smo
već vidjeli.
Bez dokaza navodimo sljedeće tvrdnje:
- i)
- plošni integral skalarnog polja ne ovisi ni o parametrizaciji plohe niti o
njenoj orijentaciji (vidi poglavlje 3.3),
- ii)
- plošni integral skalarnog polja je linearan, odnosno
Primjer 3.1 Izračunajmo
gdje je
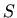
dio središnje jedinične sfere u prvom oktantu.
Ploha
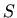
prikazana je na slici
3.5.
Slika 3.5:
Dio središnje jedinične sfere
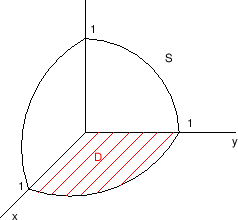 |
Plohu možemo opisati s
Dakle, područje
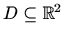
opisano je s
dok je
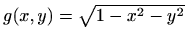
. Iz
slijedi
pa je
Glatka ploha
PLOŠNI INTEGRALI
Plošni integral vektorskog polja
![]() sastavljenoj od ploha
sastavljenoj od ploha
![]() definiramo kao
definiramo kao
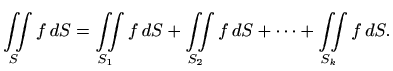
![]() površinska gustoća plohe
površinska gustoća plohe ![]() , onda
, onda
![]() daje masu
plohe. Ako stavimo
daje masu
plohe. Ako stavimo ![]() , onda
, onda
![]() daje površinu plohe kao što smo
već vidjeli.
daje površinu plohe kao što smo
već vidjeli.
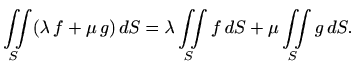
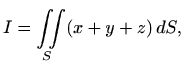
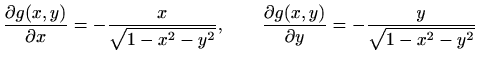
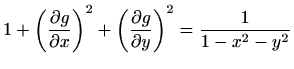
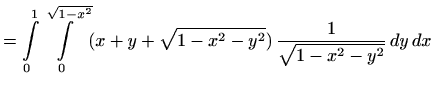
![$\displaystyle =\left\{ \begin{array}{ll}x=r\cos \varphi ,&\varphi \in[0,\pi/2] \\ y=r\sin\varphi ,&r\in[0,1] \end{array}\right\}$](img578.gif)