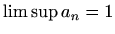 ,
,
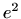
- (a)
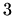 ,
,
- (b)
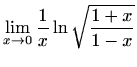 ,
,
- (c)
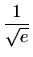 ,
,
- (d)
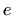 ,
,
- (e)
-
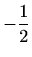 .
.
- (a)
-
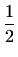 ,
,
- (b)
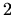 .
.
- (a)
- 0,
- (b)
- 0.
- (a)
-
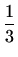 ,
,
- (b)
-
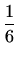 ,
,
- (c)
-
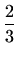 .
.
- (a)
-
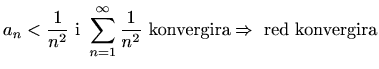 ,
,
- (b)
-
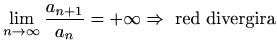 .
.
- (a)
-
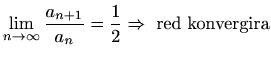 ,
,
- (b)
-
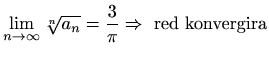 .
.
- (a)
-
![$ \displaystyle
\lim_{n\to\infty}\sqrt[n]{a_n}=\displaystyle\frac{3}{\pi} \Rightarrow\textrm{ red konvergira}$](img3409.gif) ,
,
- (b)
-
![$ \displaystyle
\lim_{n\to\infty}\sqrt[n]{a_n}=+\infty \Rightarrow\textrm{ red divergira}$](img3410.gif) .
.
- (a)
-
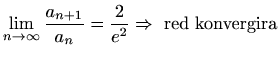 ,
,
- (b)
-
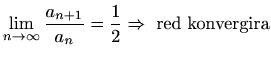 ,
,
- (c)
-
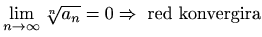 ,
,
- (d)
-
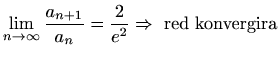 ,
,
- (e)
-
![$ \displaystyle \lim_{n\to\infty}\sqrt[n]{a_n}=0 \Rightarrow\textrm{ red konvergira}$](img3413.gif) ,
,
- (f)
-
![$ \displaystyle \lim_{n\to\infty}\sqrt[n]{a_n}=\frac{1}{e} \Rightarrow\textrm{ red konvergira}$](img3414.gif) ,
,
- (g)
-
![$ \displaystyle \lim_{n\to\infty}\sqrt[n]{a_n}=e^2 \Rightarrow\textrm{ red divergira}$](img3415.gif) ,
,
- (h)
-
![$ \displaystyle \lim_{n\to\infty}\sqrt[n]{a_n}=\frac{1}{2}\Rightarrow\textrm{ red konvergira}$](img3416.gif) .
.
![$ \displaystyle \lim_{n\to\infty}\sqrt[n]{a_n}=\frac{1}{a}\Rightarrow\textrm{red konvergira za } a>1, \textrm{divergira za } a<1$](img3417.gif) .
.
Za ![]() je
je
![]() pa red divergira.
pa red divergira.
- (a)
-
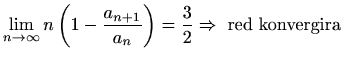 ,
,
- (b)
-
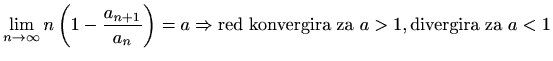 .
.
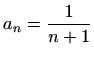 .
.
Za ![]() je
je
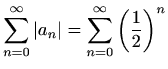 pa red divergira.
pa red divergira.
- (a)
-
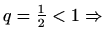 je geometrijski red za
je geometrijski red za
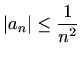 red apsolutno konvergira
red apsolutno konvergira
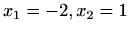 red konvergira,
red konvergira,
- (b)
-
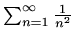 i
i
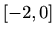 konvergira
konvergira
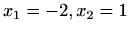 red apsolutno konvergira
red apsolutno konvergira
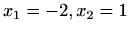 red konvergira.
red konvergira.
- (a)
-
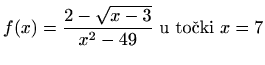 ,
,
- (b)
![$ [-2,0]$](img3427.gif) ,
,
- (c)
-
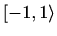 ,
,
- (d)
-
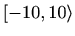 ,
,
- (e)
-
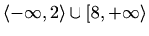 ,
,
- (f)
-
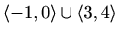 ,
,
- (g)
-
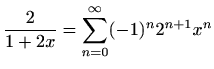 .
.
- (a)
-
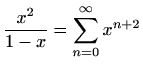 ,
,
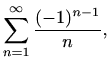 ,
,
- (b)
-
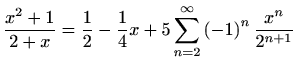 ,
,
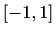 ,
,
- (c)
-
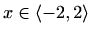 ,
,
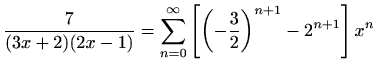 ,
,
- (d)
-
![$ \displaystyle \frac{7}{(3x+2)(2x-1)}=\sum\limits_{n=0}^{\infty}\left[\left(-\frac{3}{2}\right)^{n+1}-2^{n+1}\right]x^n$](img3437.gif) ,
,
![$ x\in \left\langle-\frac{1}{2},\frac{1}{2}\right]$](img3438.gif)
- (a)
-
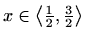 ,
,
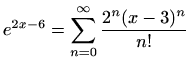 ,
,
- (b)
-
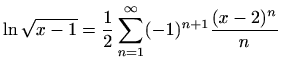 ,
,
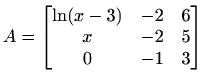 ,
,
- (c)
-
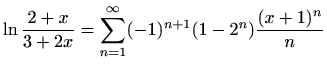 ,
,
![$ x\in\langle 1,3]$](img3285.gif) ,
,
- (d)
-
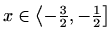 ,
,
![$ x\in\left\langle-\frac{3}{2},-\frac{1}{2}\right]$](img3444.gif) ,
,
- (e)
-
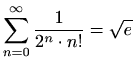 ,
,
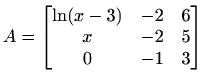 .
.
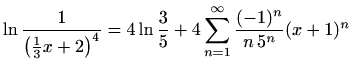 .
.
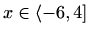 ,
,
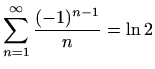 .
.