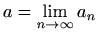
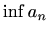
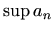
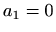
Odredite konstante ![]() i
i ![]() takve da je
takve da je
![]() i
i ![]()
- (a)
-
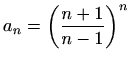 ,
,
- (b)
-
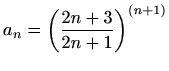 ,
,
- (c)
-
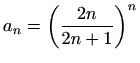 ,
,
- (d)
-
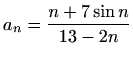 ,
,
- (e)
-
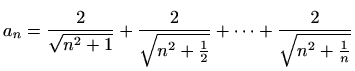 .
.
- (a)
-
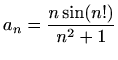 ,
,
- (b)
-
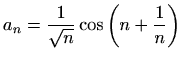 .
.
- (a)
-
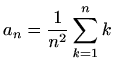 ,
,
- (b)
-
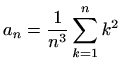 .
.
- (a)
-
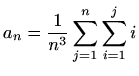 ,
,
- (b)
-
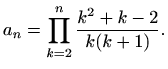 ,
,
- (c)
-
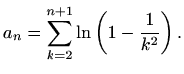 ,
,
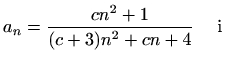
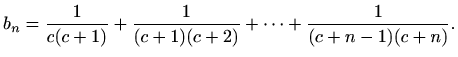
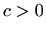
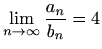
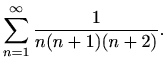
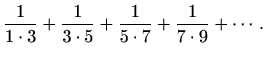
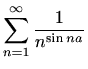
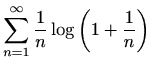
- (a)
-
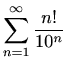 ,
,
- (b)
-
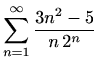 .
.
- (a)
-
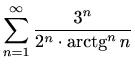 ,
,
- (b)
-
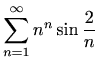 .
.
- (a)
-
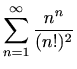 ,
,
- (b)
-
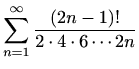 .
.
- (a)
-
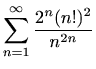 ,
,
- (b)
-
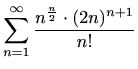 ,
,
- (c)
-
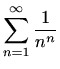 ,
,
- (d)
-
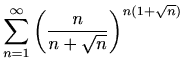 ,
,
- (e)
-
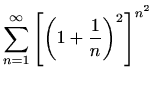 ,
,
- (f)
-
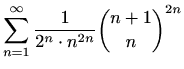 ,
,
- (g)
-
![$ \displaystyle \sum_{n=1}^\infty \left[\left(1+\frac{1}{n}\right)^2\right]^{n^2}$](img3355.gif) ,
,
- (h)
-
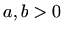 .
.
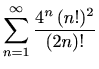
- (a)
-
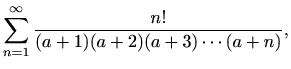 ,
,
- (b)
-
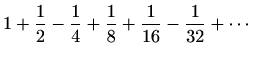 .
.
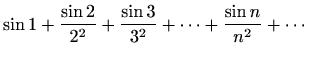
- (a)
-
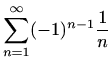 ,
,
- (b)
-
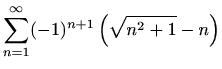 .
.
- (a)
-
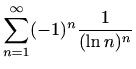 ,
,
- (b)
-
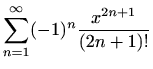 ,
,
- (c)
-
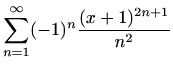 .
.
- (a)
-
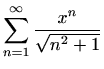 ,
,
- (b)
-
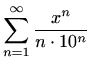 ,
,
- (c)
-
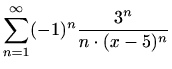 ,
,
- (d)
-
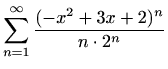 ,
,
- (e)
-
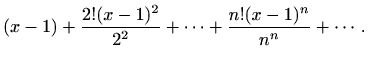 ,
,
- (f)
-
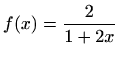 .
.
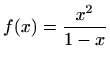
- (a)
-
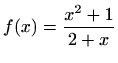 ,
,
- (b)
-
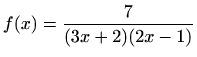 ,
,
- (c)
-
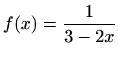 ,
,
- (d)
-
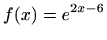 .
.
- (a)
-
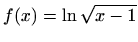 i
i 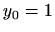 ,
,
- (b)
-
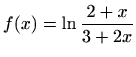 i
i 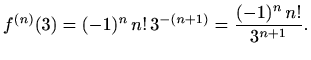 ,
,
- (c)
-
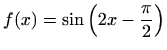 i
i 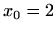 ,
,
- (d)
-
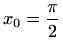 i
i 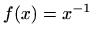 ,
,
- (e)
-
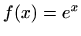 i
i
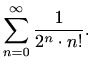 ,
,
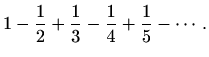 |
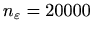 ,
odredite područje konvergencije dobivenog reda i izračunajte sumu reda
,
odredite područje konvergencije dobivenog reda i izračunajte sumu reda
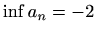 |