Suma reda s logaritmima

Izračunajte sumu reda

$\displaystyle \displaystyle \sum_{n=2}^\infty \ln\left(\frac{n^3-1}{n^3+1}\right).$

Rješenje. Zbog svojstava logaritamske funkcije vrijedi

$\displaystyle s_k = \sum_{n=2}^k \ln\left(\frac{n^3-1}{n^3+1}\right) = \ln\prod_{n=2}^k \frac{n^3-1}{n^3+1}.$

Nadalje, zbroj i razliku kubova možemo rastaviti na faktore

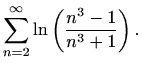
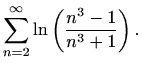
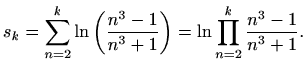
$\displaystyle \frac{n^3-1}{n^3+1} = \frac{(n-1)(n^2+n+1)}{(n+1)(n^2-n+1)} = \frac{(n-1)(n^2+n+1)}{(n+1)\left[(n-1)^2+(n-1)+1\right]}$

pa skraćivanjem dobivamo

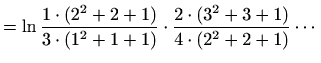
$\displaystyle s_k$	$\displaystyle = \ln \frac{1\cdot (2^2+2+1)}{3\cdot (1^2+1+1)} \cdot \frac{2 \cdot (3^2+3+1)}{4\cdot (2^2+2+1)}\cdots$
	$\displaystyle \cdots\frac{(k-2)\left[(k-1)^2+(k-1)+1\right]}{k\left[(k-2)^2+(k-... ...t]} \cdot \frac{(k-1)\left[k^2+k+1\right]} {(k+1)\left[(k-1)^2+(k-1)+1\right]}=$
	$\displaystyle = \ln\left[\frac{1\cdot 2}{1^2+1+1} \cdot \frac{k^2+k+1}{k(k+1)}\right]= \ln\left[\frac{2}{3} \left(1+\frac{1}{k^2+k}\right)\right] .$

Prema

[M1, definicija 6.9], suma reda je jednaka

$\displaystyle s=\lim_{k\to \infty} s_k$

$\displaystyle =\lim_{k\to \infty}\ln\left[\frac{2}{3} \left(1+\frac{1}{k^2+k}\r... ... \infty}\left[\frac{2}{3} \left(1+\frac{1}{k^2+k}\right)\right]=\ln\frac{2}{3}.$