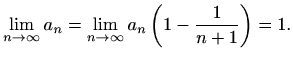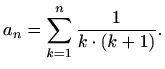
Izračunajte limes niza čiji je opći član
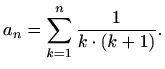
Rješenje. Rastavimo izraz pod sumom na parcijalne razlomke, odnosno
nađimo konstante ![]() i
i ![]() takve da za svaki
takve da za svaki
![]() vrijedi
vrijedi
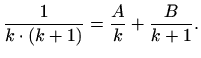
Množenjem jednakosti sa zajedničkim nazivnikom i sređivanjem slijedi
Budući da dobivena jednakost vrijedi za sve
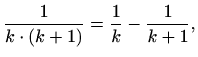
pa je
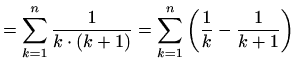 |
||
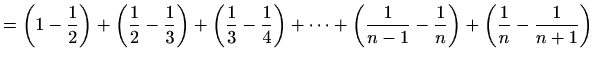 |
||
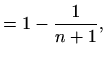 |