Hiperbolne funkcije
definiramo pomoću eksponencijalne
funkcije ![]() (poglavlje 4.6.3). Hiperbolne funkcije su zanimljive jer
su rješenja mnogih problema u fizici i tehnici izražena pomoću njih.
Veze između hiperbolnih funkcija
slične su vezama između trigonometrijskih
funkcija.
(poglavlje 4.6.3). Hiperbolne funkcije su zanimljive jer
su rješenja mnogih problema u fizici i tehnici izražena pomoću njih.
Veze između hiperbolnih funkcija
slične su vezama između trigonometrijskih
funkcija.
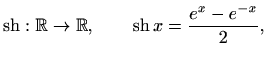
a kosinus hiperbolni je funkcija
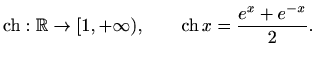
Funkcije
Vidimo da je sinus hiperbolni neparna, a
kosinus hiperbolni parna funkcija te da je sinus hiperbolni
strogo rastuća funkcija.
Kosinus hiperbolni se još zove i lančanica,
jer lanac obješen o
dvije točke u gravitacijskom polju zauzme oblik dijela te krivulje.
Za funkcije
![]() i
i
![]() vrijedi
vrijedi
Slično kao kod trigonometrijskih funkcija, tangens hiperbolni definiramo kao kvocijent sinusa i kosinusa, a kotangens hiperbolni kao kvocijent kosinusa i sinusa, odnosno
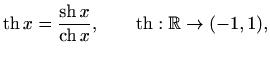 |
||
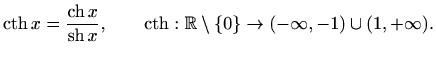 |
Funkcije
![]() i
i
![]() prikazane su na slici 4.40.
Funkcija
prikazane su na slici 4.40.
Funkcija
![]() je neparna, strogo rastuća i neprekidna te
ima horizontalne asimptote
je neparna, strogo rastuća i neprekidna te
ima horizontalne asimptote ![]() i lijevom i
i lijevom i ![]() u desnom kraju.
Funkcija
u desnom kraju.
Funkcija
![]() je neparna, strogo padajuća i ima prekid druge
vrste u točki
je neparna, strogo padajuća i ima prekid druge
vrste u točki ![]() . Njene horizontalne asimptote su također pravci
. Njene horizontalne asimptote su također pravci
![]() i lijevom i
i lijevom i ![]() u desnom kraju, a pravac
u desnom kraju, a pravac ![]() je vertikalna
asimptota s obje strane.
je vertikalna
asimptota s obje strane.
Area funkcije
su inverzne funkcije hiperbolnih funkcija.
Primijetimo da su sve hiperbolne funkcije bijekcije, osim
![]() pa
za kosinus hiperbolni inverznu funkciju definiramo za restrikciju
pa
za kosinus hiperbolni inverznu funkciju definiramo za restrikciju
![]() . Funkcije
area sinus hiperbolni,
area kosinus hiperbolni,
area tangens hiperbolni i
area kotangens hiperbolni
definirane su redom na sljedeći način:
. Funkcije
area sinus hiperbolni,
area kosinus hiperbolni,
area tangens hiperbolni i
area kotangens hiperbolni
definirane su redom na sljedeći način:
Area funkcije se ponekad označavaju i s velikim početnim slovom kao na
primjer
![]() . Funkcije
. Funkcije
![]() i
i
![]() prikazane su na
slici 4.41, a funkcije
prikazane su na
slici 4.41, a funkcije
![]() i
i
![]() na
slici 4.42.
na
slici 4.42.