×   HOME PREDAVANJA

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI INDEKS

VJEŽBE

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

KVIZ

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

PODSJETNIK

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

JAVA NETPLOT OCTAVE Traži ...

☰   matematika1 Aritmetika računala     Realni brojevi     Kompleksni brojevi

Apsolutna vrijednost

U ovom poglavlju definirat ćemu apsolutnu vrijednost realnog broja i dokazati neka njena svojstva.

Definicija 1.18   Apsolutna vrijednost realnog broja je funkcija $\vert\phantom{x}\vert:\mathbb{R}\to [0,+\infty)$ definirana s

$$% \vert x\vert=\begin{cases}x,& \text{za $x\geq 0$,}\\ -x,&\text{za $x<0$.} \end{cases}$$

Na primjer,

$$% \vert\vert=0,\quad \vert 5\vert=\vert-5\vert=5,\quad \vert x\vert=\vert-x\vert,\quad \vert x-y\vert=\vert y-x\vert.$$

Na slici 1.1 prikazan je graf funkcije $\vert x\vert$ . Graf funkcije $y=f(x)$ definiramo kao skup svih točaka $xy$ -ravnine za koje je $y=f(x)$ . Preciznije definicije funkcije i grafa dane su u poglavlju 4.

Slika 1.1: Apsolutna vrijednost $\vert x\vert$

Teorem 1.10   Za apsolutnu vrijednost vrijedi:

i)

$\vert x\vert<r\quad\Leftrightarrow\quad -r<x<r\quad \Leftrightarrow \quad x\in(-r,r)$ ;

ii)

nejednakost trokuta, $\vert x+y\vert\leq \vert x\vert+\vert y\vert$ , odnosno općenitije

$$% \left\vert \sum_{i=1}^n x_i \right\vert \leq \sum_{i=1}^n \vert x_i\vert;$$

iii)

$\vert x-y\vert\geq \vert x\vert-\vert y\vert$ ;

iv)

$\vert x\cdot y\vert=\vert x\vert\cdot \vert y\vert$ , odnosno općenitije

$$% \left\vert \prod_{i=1}^n x_i \right\vert = \prod_{i=1}^n \vert x_i\vert;$$

v)

$$\left\vert \frac{x}{y}\right\vert=\frac{\vert x\vert}{\vert y\vert}$$ za $y\neq 0$ .

Dokaz.

i)

Za $x\geq 0$ nejednakost $\vert x\vert<r$ povlači $x<r$ , a za $x<0$ nejednakost $\vert x\vert<r$ povlači $-x<r$ , odnosno $-r<x$ .

ii)

Za svaki $x\in \mathbb{R}$ vrijedi $x\leq \vert x\vert$ . Ako je $x+y\geq 0$ , tada je $\vert x+y\vert=x+y\leq \vert x\vert+\vert y\vert$ , a ako je $x+y<0$ , tada je

$$% \vert x+y\vert=-(x+y)=-x-y\leq \vert-x\vert+\vert-y\vert=\vert x\vert+\vert y\vert$$

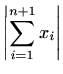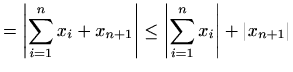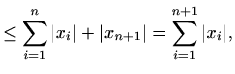pa je prva tvrdnja dokazana. Općenitiju tvrdnju dokazujemo indukcijom (vidi primjer 1.3 i dokaz teorema 1.6). Tvrdnja očito vrijedi za $n=1$ i $n=2$ . Za $n\geq 2$ imamo

$$\left\vert \sum_{i=1}^{n+1} x_i \right\vert = \left\vert \sum_{i=1}^{n} x_i +x_{n+1}\right\vert \leq \left\vert \sum_{i=1}^{n} x_i \right\vert +\vert x_{n+1}\vert$$

$$\leq \sum_{i=1}^n \vert x_i\vert + \vert x_{n+1}\vert=\sum_{i=1}^{n+1} \vert x_i\vert,$$

pa nejednakost trokuta vrijedi za svaki $n\in \mathbb{N}$ .     

Q.E.D.

Zadatak 1.4   Dokažite tvrdnje iii), iv) i v) teorema 1.10.

Aritmetika računala     Realni brojevi     Kompleksni brojevi