Cijeli brojevi

U ovom poglavlju ukratko ćemo dati osnovnu motivacija za uvođenje skupa cijelih brojeva $\mathbb{Z}$ te navesti osnovna svojstva tog skupa.

Prema definiciji 1.14 za $m,n\in \mathbb{N}$ vrijedi

$\displaystyle % m<n \Leftrightarrow (\exists p\in \mathbb{N})\quad m+p=n.$

Kako je broj

jedinstven, možemo pisati

. Ako je pak

, tada $n-m\notin \mathbb{N}$ . Stoga skup prirodnih brojeva $\mathbb{N}$ proširujemo s njegovom negativnom kopijom i dodajemo element 0 za koji vrijedi

$\displaystyle % 0\cdot m=0 \quad \textrm{i} \quad 0+m=m, \quad \forall m\in \mathbb{Z}.$

Uređaj na skupu $\mathbb{Z}$ uvodimo slično kao u definiciji 1.14. Skup $(\mathbb{Z},\leq)$ je diskretan kao i skup $\mathbb{N}$ , a razlikuju se u tome što $\mathbb{Z}$ nema najmanji element.

Skup $\mathbb{Z}$ je ekivipotentan s $\mathbb{N}$ , odnosno oba skupa imaju jednako mnogo elemenata, jer je funkcija $f:\mathbb{N}\to \mathbb{Z}$ definirana s

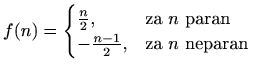
$\displaystyle % f(n)=\begin{cases}\frac{n}{2},& \text{za $n$\ paran} \\ -\frac{n-1}{2}, & \text{za $n$\ neparan} \end{cases}$

bijekcija.

Računske operacije , i $\cdot$ na skupu $\mathbb{Z}$ definiramo na poznati način te za njih vrijede svojstva slično kao u Teoremu 1.3.