Svojstva limesa

Svojstva limesa nizova slična su svojstvima limesa funkcija koja su dana u poglavlju 4.3.1. Dokaz sljedećeg teorema sličan je dokazu teorema 4.3 pa ga stoga izostavljamo.

Teorem 6.6 Neka su nizovi $\{a_n\}$ i $\{b_n\}$ konvergentni. Tada vrijedi:

i)

$\lim (a_n+b_n)=\lim (a_n)+\lim(b_n)$ ,

ii)

$\lim (a_n-b_n)=\lim (a_n)-\lim(b_n)$ ,

iii)

$\lim (a_n \cdot b_n)=\lim (a_n) \cdot \lim(b_n)$ ,

iv)

ako za svaki

vrijedi $b_n\neq 0$ i ako je $\lim b_n\neq 0$ , tada je

$\displaystyle % \lim\frac{a_n}{b_n}=\frac{\lim a_n}{\lim b_n},$

v)

ako za svaki

vrijedi

i ako je $\lim a_n > 0$ , tada je

$\displaystyle % \lim a_n\, ^{\displaystyle b_n}=(\lim a_n)^{\displaystyle \lim b_n}.$

Posebno, ako je

stacionaran niz,

, tada je

$\displaystyle % \lim (a_n)^x = (\lim a_n)^x.$

Primjer 6.5

a)

Za niz

$\displaystyle % a_n =\frac{an+b}{cn+d}, \quad a,b,c,d\in \mathbb{R}, \quad c\neq 0,$

vrijedi

$\displaystyle % \lim a_n=\lim\frac{(an+b)\cdot\frac{1}{n}}{(cn+d)\cdot\frac{1}{... ...lim\left(a+\frac{b}{n}\right)}{\lim\left(c+\frac{d}{n}\right)} = \frac{a}{c}.$

b)

Za niz

$\displaystyle % a_n=\sum_{k=1}^{n} \frac{k}{n^2},$

odnosno

$\displaystyle % a_1=1,\quad a_2=\frac{1}{4}+\frac{2}{4},\quad a_3=\frac{1}{3^2}+\frac{2}{3^2}+ \frac{3}{3^2}, \quad \ldots,$

vrijedi

$\displaystyle % \lim a_n=\lim\frac{\frac{1}{2}n(n+1)}{n^2} = \lim\frac{1}{2}\cdot \lim\frac{n+1}{n} =\frac{1}{2}.$

Teorem 6.7 Ako za nizove $\{a_n\}$ , $\{b_n\}$ i $\{c_n\}$ postoji $n_0\in \mathbb{N}$ takav da $n\geq n_0$ povlači $a_n\leq b_n \leq c_n$ i ako je $\lim a_n=\lim c_n = a$ , tada je i $\lim b_n=a$ .

Primjer 6.6 Pokažimo

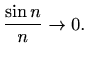
$\displaystyle % \frac{\sin n}{n}\to 0.$

Zaista, budući je $-1\leq \sin n\leq 1$ , to za svaki $n\in \mathbb{N}$ vrijedi

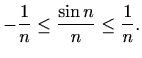
$\displaystyle % -\frac{1}{n} \leq \frac{\sin n}{n} \leq \frac{1}{n}.$

Kako $-\frac{1}{n}\to 0$ i $\frac{1}{n}\to 0$ , tvrdnja slijedi iz teorema 6.7.