☰
matematika1
Površina i duljina dijagonala
VEKTORSKA ALGEBRA I ANALITIČKA
Volumen paralelopipeda
Mješoviti produkt
Zadani su vektori
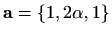 ,
,
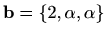 i
i
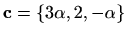 .
.
- a)
- Izračunajte mješoviti produkt vektora
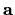 ,
,
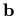 i
i
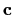 .
.
- b)
- Odredite
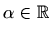 takav da su vektori
takav da su vektori
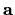 ,
,
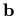 i
i
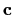 komplanarni.
komplanarni.
Rješenje.
- a)
- Prema
![[*]](../icons.gif/crossref.gif) [M1, teorem 3.4], mješoviti produkt vektora
[M1, teorem 3.4], mješoviti produkt vektora
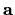 ,
,
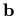 i
i
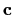 je
je
- b)
- Prema
![[*]](../icons.gif/crossref.gif) [M1, poglavlje 3.11], vektori
[M1, poglavlje 3.11], vektori
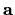 ,
,
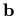 i
i
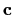 su komplanarni ako vrijedi
su komplanarni ako vrijedi
odnosno ako je
Ova jednadžba ima samo jedno realno rješenje 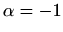 .
.