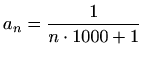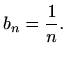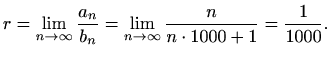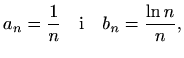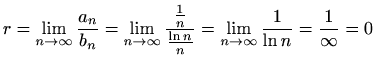Drugi poredbeni kriterij konvergencije

Ispitajte konvergenciju reda:

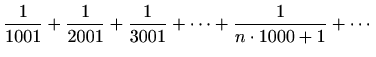a): $\displaystyle \frac{1}{1001}+\frac{1}{2001}+\frac{1}{3001}+\cdots+\frac{1}{n\cdot 1000+1}+\cdots$ ,
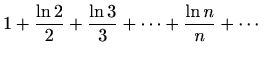b): $\displaystyle 1+\frac{\ln 2}{2}+\frac{\ln 3}{3}+\cdots+\frac{\ln n}{n}+\cdots$ .

Rješenje.

a)

Usporedimo zadani red čiji je opći član

$\displaystyle a_n=\frac{1}{n\cdot 1000+1}$

s redom čiji je opći član

$\displaystyle b_n=\frac{1}{n}.$

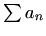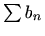Tada su $\sum a_n$ i $\sum b_n$ redovi s pozitivnim članovima i vrijedi

$\displaystyle r=\lim_{n\to \infty} \frac{a_n}{b_n}=\lim_{n\to \infty} \frac{n}{n\cdot 1000+1}=\frac{1}{1000}.$

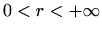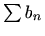Jer je $0<r<+\infty$ i $\sum b_n$ harmonijski red iz

[M1, primjer 6.10] koji divergira, tvrdnja (ii) pod (a) iz

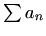[M1, teorem 6.10] povlači da i zadani red $\sum a_n$ divergira.

b)

Uz oznake

$\displaystyle a_n=\frac{1}{n} \quad\textrm{i}\quad b_n=\frac{\ln n}{n},$

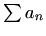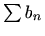su $\sum a_n$ i $\sum b_n$ redovi s pozitivnim članovima. Jer je

$\displaystyle r=\lim_{n\to \infty} \frac{a_n}{b_n}=\lim_{n\to \infty} \frac{\frac{1}{n}}{\frac{\ln n}{n}}= \lim_{n\to \infty} \frac{1}{\ln n}=\frac{1}{\infty}=0$

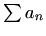i $\sum a_n$ divergentan harmonijski red, prema tvrdnji (ii) pod (b) iz

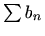[M1, teorem 6.10], zadani red $\sum b_n$ divergira.

Prvi poredbeni kriterij konvergencije NIZOVI I REDOVI D'Alembertov kriterij konvergencije
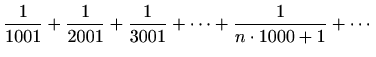
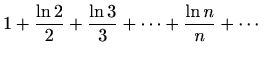
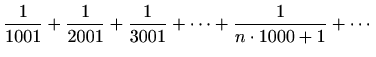
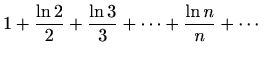