Tok funkcije IV

Ispitajte tok i skicirajte graf funkcije zadane s

$\displaystyle f(x)=2\sin(2x)+\sin(4x)$

bez računanja točaka infleksije i intervala zakrivljenosti.

Rješenje.

Područje definicije
Domena funkcije je $\mathcal{D}(f)=\mathbb{R}$ .
Parnost
Vrijedi

$\displaystyle f(-x)=2\sin(-2x)+\sin(-4x)=-2\sin(2x)-\sin(4x)=-f(x),$

pa je funkcija neparna.
Periodičnost
Funkcija je periodična s periodom $\pi$ jer vrijedi

$\displaystyle f(x+\pi)=2\sin(2x+2\pi)+\sin(4x+4\pi)=2\sin(2x)+\sin(4x)=f(x)$

i to je najmanji broj s tim svojstvom. Stoga je dovoljno ispitati tok funkcije na intervalu $[0,\pi\rangle$ .
Nul-točke
Riješimo jednadžbu za $x\in[0,\pi\rangle.$ Zbog

$\displaystyle f(x)=2\sin(2x)+\sin(4x)=2\sin(2x)+2\sin(2x)\cos(2x)=2\sin(2x)[1+\cos(2x)]$

imamo dva slučaja

$\displaystyle \sin(2x)=0\quad\textrm{ ili }\quad \cos(2x)=-1.$

Dakle, nul-točke iz $[0,\pi\rangle$ su i $x_1=\frac{\pi}{2}$ .
Asimptote
Vertikalnih asimptota nema jer je $\mathcal{D}(f)=\mathbb{R}$ , a horizontalne i kose nećemo tražiti budući da ispitujemo tok funkcije samo na $[0,\pi\rangle$ .
Ekstremi
Odredimo prvo stacionarne točke. Zbog

$\displaystyle f^\prime (x)=4\left[\cos(2x)+\cos(4x)\right]=4[\cos(2x)+2\cos^2(2x)-1],$

uvjet $f^\prime(x)=0$ i supstitucija $t=\cos(2x)$ daju kvadratnu jednadžbu

$\displaystyle 2t^2+t-1=0$

koja ima rješenja i $t_2=\frac{1}{2}$ , pa stacionarne točke zadovoljavaju

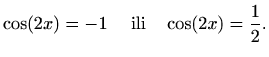$\displaystyle \cos(2x) =-1\quad \textrm{ ili} \quad \cos(2x)=\frac{1}{2}.$

Rješenja iz $[0,\pi\rangle$ su

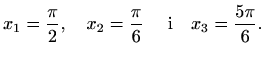
$\displaystyle x_1=\frac{\pi}{2},\quad x_2=\frac{\pi}{6} \quad \textrm{ i} \quad x_3=\frac{5\pi}{6}.$

Još primijetimo da funkcija nema točaka u kojima $f^\prime$ nije definirana. Lokalne ekstreme odredimo prema predznaku druge derivacije u dobivenim stacionarnim točkama. Vrijedi

$\displaystyle f^{\prime\prime}(x)=-8\left[\sin(2x)+2\sin(4x)\right].$

Stoga

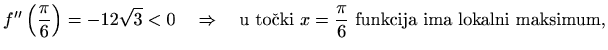$\displaystyle f^{\prime\prime}\left(\frac{\pi}{6}\right) =-12\sqrt{3}<0 \quad\Rightarrow\quad \textrm{u točki $x=\frac{\pi}{6}$ funkcija ima lokalni maksimum},$

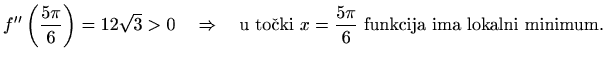$\displaystyle f^{\prime\prime}\left(\frac{5\pi}{6}\right) =12\sqrt{3}>0 \quad\Rightarrow\quad \textrm{u točki $x=\frac{5\pi}{6}$\ funkcija ima lokalni minimum.}$

Nadalje,

$\displaystyle f'''(x)=-16[\cos(2x)+4\cos(4x)],$

pa zbog

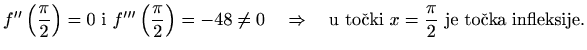
$\displaystyle f^{\prime\prime}\left(\frac{\pi}{2}\right) =0 \textrm{ i } f'''\l... ...\quad\Rightarrow\quad \textrm{u točki $x=\frac{\pi}{2}$ je točka infleksije}.$
Intervali monotonosti
Točke , i dijele interval $[0,\pi\rangle$ na četiri dijela i dovoljno je na svakom od njih ispitati predznak prve derivacije u proizvoljno odabranoj točki jer se on ne mijenja unutar intervala.

a)

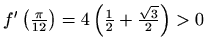Za $\left[0,\frac{\pi}{6}\right\rangle$ je $f^\prime\left(\frac{\pi}{12}\right)=4\left(\frac{1}{2}+\frac{\sqrt{3}}{2}\right)>0$ .

b)

Za $\left[\frac{\pi}{6},\frac{\pi}{2}\right\rangle$ je $f^\prime\left(\frac{\pi}{3}\right)=-4<0$ .

c)

Za $\left[\frac{\pi}{2},\frac{5\pi}{6}\right\rangle$ je $f^\prime \left(\frac{2\pi}{3}\right)=-4<0$ .

d)

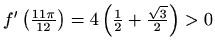Za $\left[\frac{5\pi}{6},\pi\right\rangle$ je $f^\prime \left(\frac{11\pi}{12}\right)= 4\left(\frac{1}{2}+\frac{\sqrt{3}}{2}\right)>0$ .

Slijedi da je rastuća na intervalima $\left[0,\frac{\pi}{6}\right\rangle$ i $\left[\frac{5\pi}{6},\pi\right\rangle$ , a padajuća na intervalu $\left[\frac{\pi}{6},\frac{5\pi}{6}\right\rangle$ .
Graf funkcije
Graf funkcije je prikazan na slici 5.8. Skiciramo prvo dio grafa na intervalu $[0,\pi\rangle$ i dalje proširimo po periodičnosti.

**Slika 5.8:** Graf funkcije $f(x)=2\sin (2x)+\sin (4x)$ .
$\begin{figure} % latex2html id marker 15947 \begin{center} \epsfig{file=derivacije/zad524.eps, width=9cm}\end{center}\end{figure}$

Tok funkcije III DERIVACIJE I PRIMJENE Zadaci za vježbu

	$\displaystyle f^{\prime\prime}\left(\frac{\pi}{6}\right) =-12\sqrt{3}<0 \quad\Rightarrow\quad \textrm{u točki $x=\frac{\pi}{6}$ funkcija ima lokalni maksimum},$
	$\displaystyle f^{\prime\prime}\left(\frac{5\pi}{6}\right) =12\sqrt{3}>0 \quad\Rightarrow\quad \textrm{u točki $x=\frac{5\pi}{6}$\ funkcija ima lokalni minimum.}$