Duljina ili norma
vektora
![]() jednaka je
jednaka je
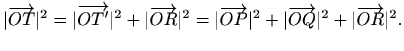
Jedinični vektor
vektora
![]() je vektor
je vektor
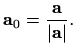
Iz definicije slijedi
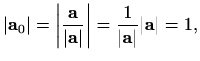
odnosno jedinični vektor ima duljinu jedan, kolinearan je vektoru
Neka je
![]() i neka su
i neka su
![]() i
i
![]() njihovi predstavnici s hvatištem u točki
njihovi predstavnici s hvatištem u točki ![]() , redom.
Kut između vektora
, redom.
Kut između vektora
![]() i
i
![]() definiramo kao
kut između usmjerenih dužina
definiramo kao
kut između usmjerenih dužina
![]() i
i
![]() ,
,
Prikloni kutovi
vektora
![]() su kutovi koje taj
vektor zatvara s vektorima
su kutovi koje taj
vektor zatvara s vektorima
![]() ,
,
![]() i
i
![]() .
Kosinusi smjerova
su kosinusi priklonih kutova.
.
Kosinusi smjerova
su kosinusi priklonih kutova.
Ako je
![]() i ako priklone
kutove označimo redom s
i ako priklone
kutove označimo redom s ![]() ,
, ![]() i
i ![]() , tada je
, tada je
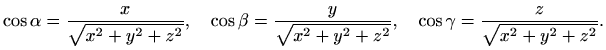
Očito je